Modal Yerdeğiştirme Talebinin Elde Edilmesi ve Performans Noktası (5B.3)
İtme analizi sonucu bina modal yerdeğiştirme talebi (performans noktası) otomatik hesaplanır.
SİMGELER
ay1 = Birinci mod için akma sözde-ivmesi [m/s2]
CR = Spektral yerdeğiştirme oranı
d1,max(X) = (X) deprem doğrultusu için modal tek serbestlik dereceli sistemin enbüyük yerdeğiştirmesi (performans noktası) [m]
fe = Taşıyıcı sistem için hesaplanan doğrusal (elastik) dayanım talebi
fy = Öngörülen süneklik kapasitesi ve periyoda bağlı akma dayanımı
Sae(T1) = Birinci doğal titreşim periyodu T1 ’e karşı gelen doğrusal elastik spektral ivme [g]
Sde(T1) = Birinci doğal titreşim periyodu T1 ’e karşı gelen doğrusal elastik spektral yerdeğiştirme [m]
Sdi(T1) = Birinci doğal titreşim periyodu T1 ’e karşı gelen doğrusal olmayan spektral yerdeğiştirme [m]
TB = Yatay elastik tasarım ivme spektrumu köşe periyodu [s]
T1 = Birinci moda ait doğal titreşim periyodu [s]
μ(Ry,T1) = Akma Dayanımı Azaltma Katsayısı ve birinci doğal titreşim periyoduna göre hesaplanan süneklik talebi
ω1(1) = Her bir k ’ıncı itme adımında yenilenen serbest titreşim hesabından bulunan birinci mod doğal açısal frekansı [rad/s]
Depremin modal yerdeğiştirme talebi ’nin elde edilmesi, verilen deprem etkisi altında modal kapasite diyagramı tarafından temsil edilen modal tek serbestlik dereceli sistemin enbüyük yerdeğiştirmesi ’nin hesabına karşı gelmektedir. Deprem etkisi Yatay Elastik Tasarım Spektrumu kullanılarak, modal tek serbestlik dereceli sistemin en büyük yerdeğiştirmesi ise itme analizi sonucu elde edile modal kapasite eğrisi kullanılarak bulunur. Depremin modal yerdeğiştirme talebi, itme eğrisinde performans noktası olarak da isimlendirilir. İtme analizinin bu noktasında elemanlarda hesaplanan plastik şekildeğiştirme değerleri sınır değerler ile karşılaştırılarak bina performansı belirlenmiş olur.
Modal tek serbestlik dereceli sistemde en büyük yerdeğiştirme, doğrusal olmayan spektral yerdeğiştirme olarak TBDY Denklem 5.12 'deki gibi tanımlanır.
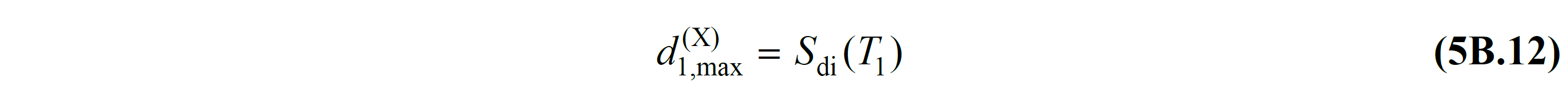
Bu denklemde d1,max(X) , modal tek serbestlik dereceli sistemin en büyük yerdeğiştirmesi 'ni, Sdi(T1) ise taşıyıcı sistemin birinci doğal titreşim periyodu T1 'e karşı gelen doğrusal olmayan spektral yerdeğiştirme 'yi ifade etmektedir. Sdi(T1) değeri TBDY Denklem 5B.13 ile tanımlanır.
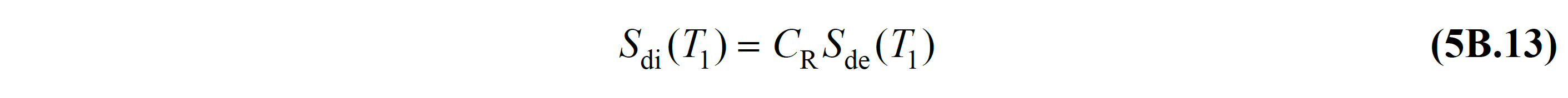
Bu denklemde Sde(T1), TBDY Denklem 2.4 ile tanımlanan birinci doğal titreşim periyoduna karşılık gelen elastik tasarım spektral yerdeğiştirmesi 'dir.
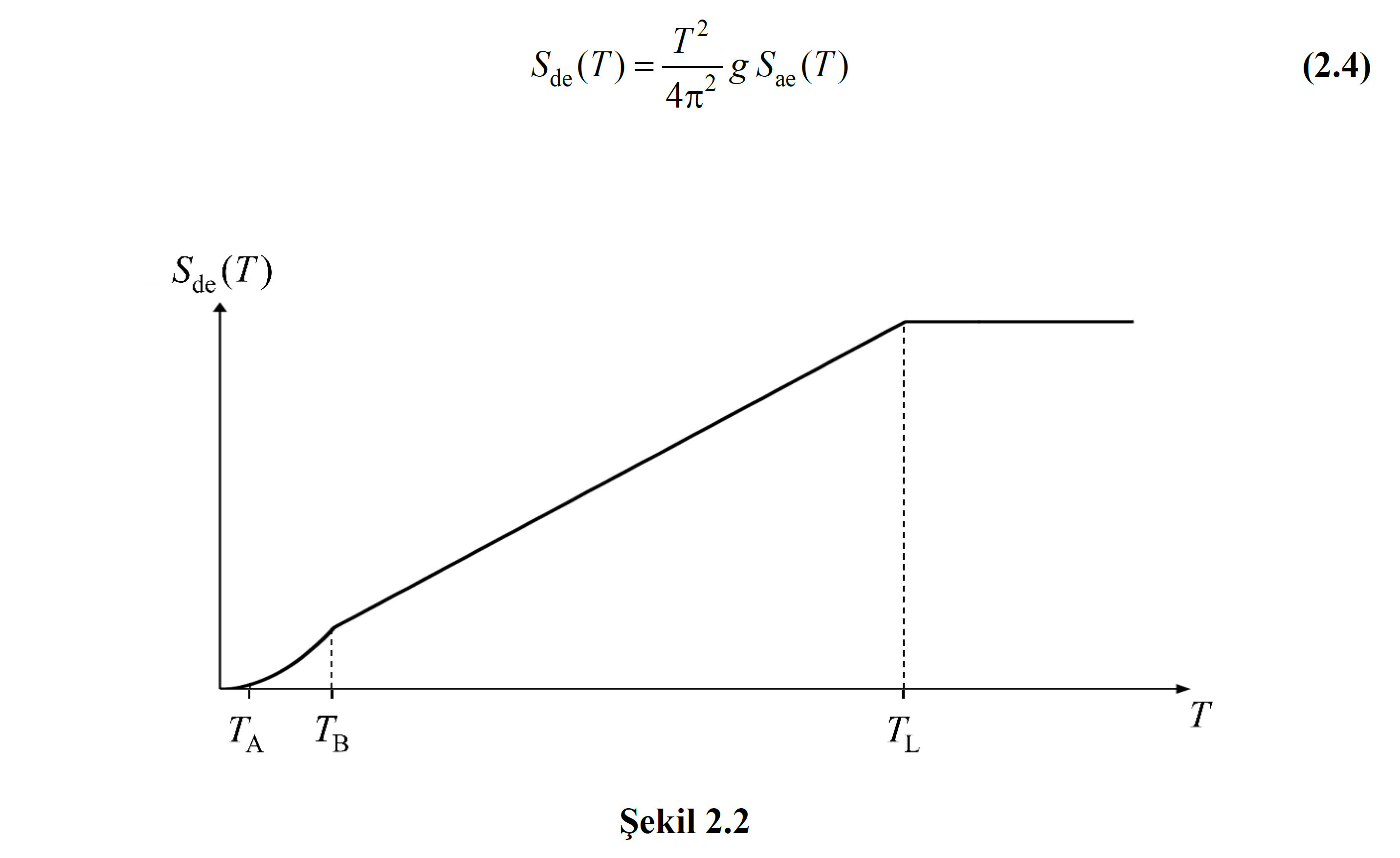
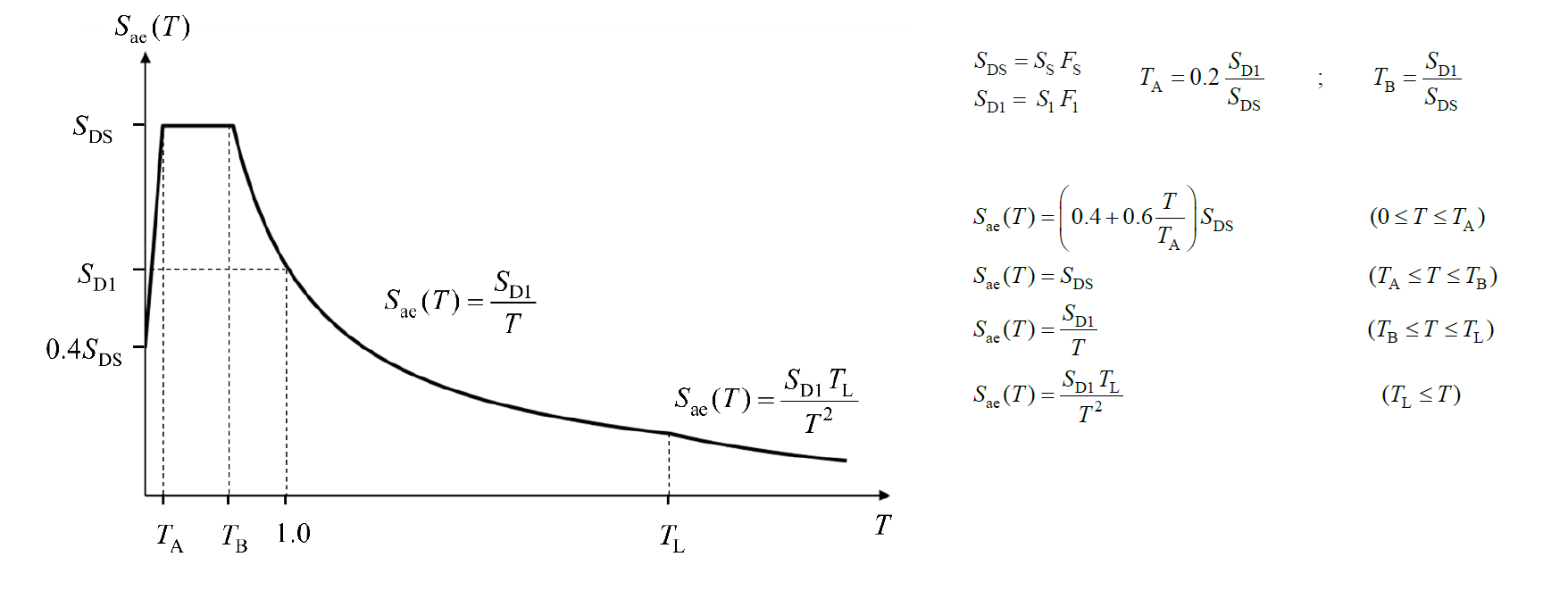
Sae(T1) değeri, Yatay Elastik Tasarım Spektrumu 'nun ordinatı olan yatay elastik tasarım spektral ivmesi 'dir.
TBDY Denklem 5B.13 'te verilen CR, spektral yerdeğiştirme oranı 'nı göstermektedir ve TBDY Denklem 5B.14 ile tanımlanır.
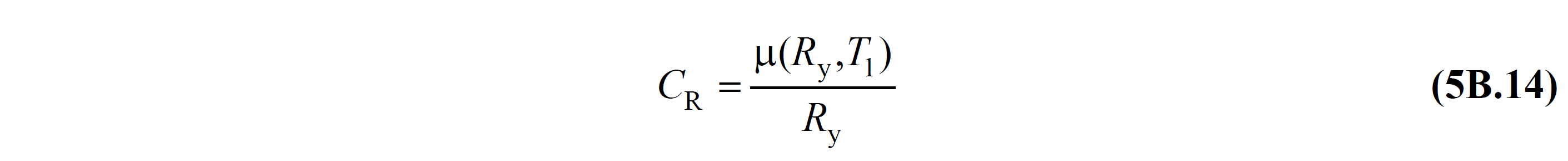
Bu denklemde Ry , akma dayanımı azaltma katsayısı 'nı göstermektedir. DGT yaklaşımında TBDY EK 4A 'da öngörülen süneklik kapasitesine bağlı olarak tanımlanan bir büyüklükten farklı olarak, ŞDGT yaklaşımında itme hesabı sonucunda akma dayanımı 'na bağlı olarak doğrudan elde edilen bir büyüklüktür ve TBDY Denklem 5B.15 ile ifade edilir.
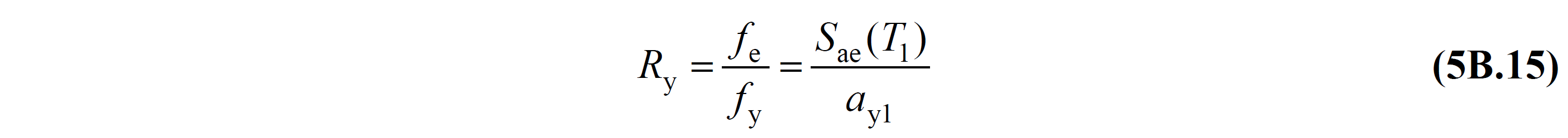
Bu bağıntıda fe ve Sae(T1) elastik dayanım talebi 'ni ve ona karşı gelen elastik spektral ivme 'yi, fy ve ay1 ise akma dayanımı 'nı ve ona karşı gelen akma sözde ivmesi 'ni temsil etmektedir (TBDY Şekil 5B.4). Bu denklemde Sae(T1) değeri koordinatları modal yerdeğiştirme - modal sözde ivme olan Yatay Elastik Tasarım Spektrumu 'nun dönüştürülmesi ile elde edilen doğrusal deprem spektrumu ordinatıdır.
TBDY Denklem 5B.14 'te yer alan μ(Ry,T1), akma dayanımı 'na ve doğal titreşim periyoduna bağlı olara ifade edilen Süneklik Talebi 'dir. Bu büyüklüğün hesabı için TBDY EK 4A 'da verilen Denklem 4A.2 'deki bağıntılar tersten yazılarak Denklem 5B.16 'daki bağıntılar elde edilebilir.
(a) Depremin süneklik talebi μ(Ry,T1), eşit yerdeğiştirme kuralı uyarınca rijitliği fazla olmayan taşıyıcı sistemler için Akma Dayanımı Azaltma Katsayısı Ry 'ye eşit alınır.

(b) Rijitliği fazla taşıyıcı sistemler için ise Denklem 4A.2b ’den Denklem 5B.16b ’deki bağıntı elde edilir:
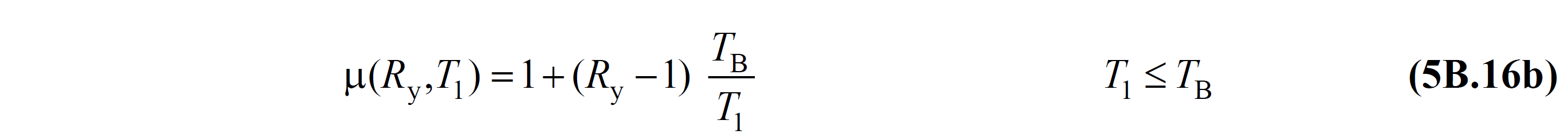
Denklem 5B.16 'daki bağıntılardan yararlanılarak Denklem 5B.14 'te tanımlanan spektral yerdeğiştirme oranı CR , TBDY Denklem 5B.17 'deki gibi ifade edilir.
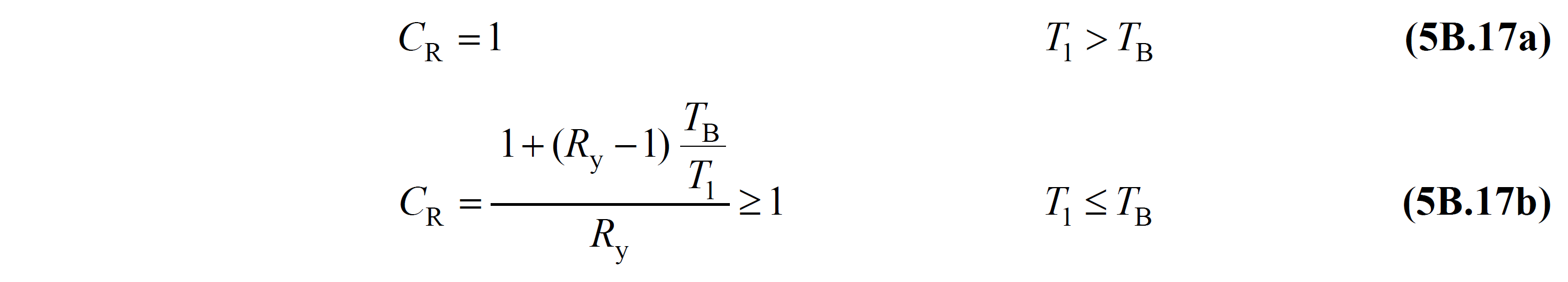
Denklem 5B.12 'de belirtilen modal tek serbestlik dereceli sistemin en büyük yerdeğiştirmesi d1,max(X) , Sabit Tek Modlu İtme Yöntemi veya Değişken Tek Modlu İtme Yöntemi kullanılarak elde edilen koordinatları modal yerdeğiştirme - modal sözde ivme olan modal kapasite diyagramı üzerinde bina performansını belirleyen performans noktasının yatay bileşenidir. Denklem 5B.12 'ye göre Yatay Elastik Tasarım Spektrumu 'nun dönüştürülmesi ile lede edilen ve koordinatları spektral yerdeğiştirme - spektral ivme (Sde , Sae) olan doğrusal deprem spektrumu 'nun yatay eksenindeki Sdi(T1) değeri ile performans noktasının modal yerdeğiştirme değeri d1,max(X) birbirine eşittir. Bu iki grafiğin üst üste çizimi TBDY Şekil 5B.3 'te gösterilmiştir.
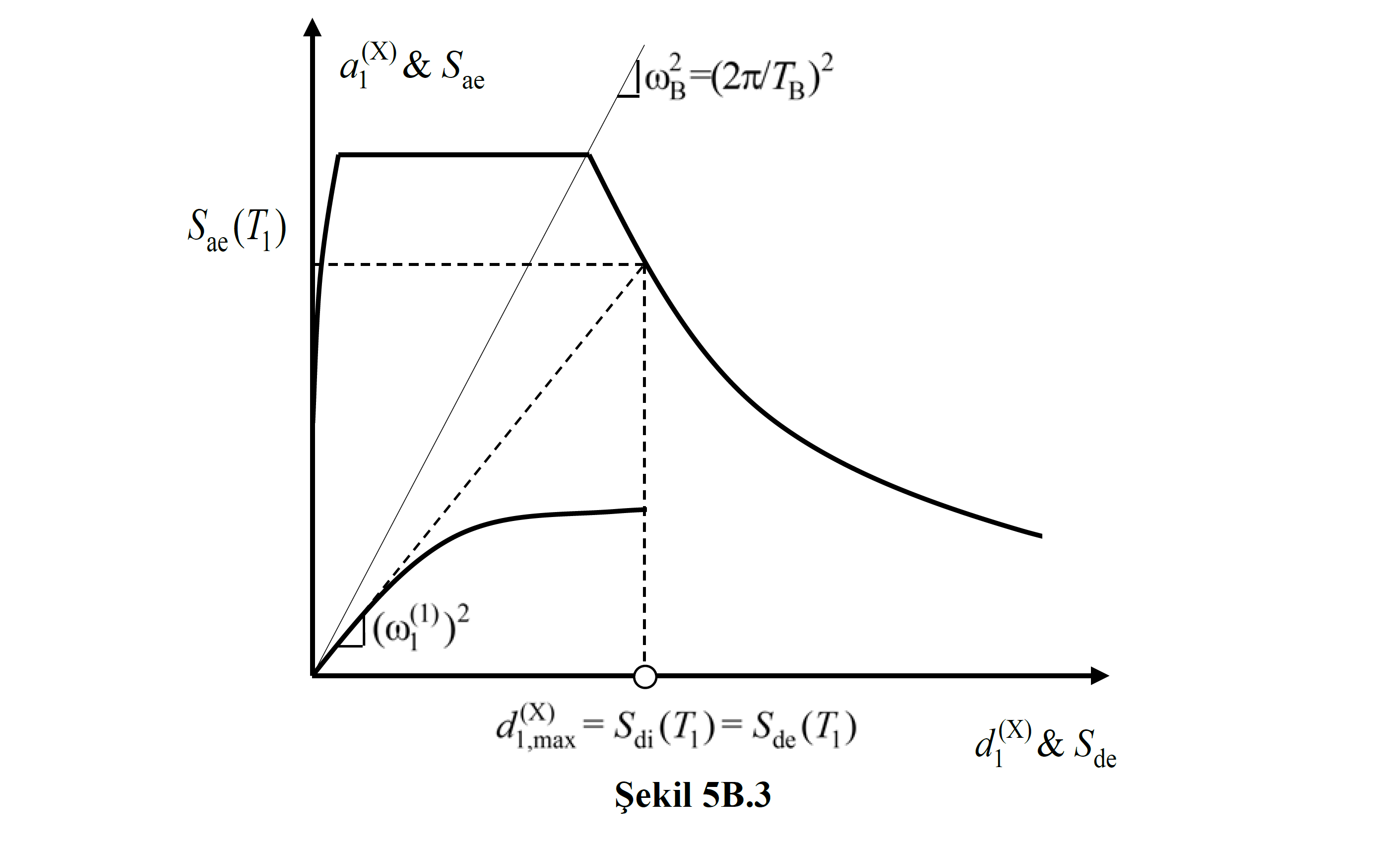
TBDY Şekil 5B.3 'te gösterilen durum, Denklem 5B.13 ile birlikte Denklem 5B.17 'nin uygulanmasına karşı gelmektedir. Bu durumda modal kapasite eğrisi üzerinde hiçbir işlem yapılmaksızın sadece birinci itme adımındaki doğal titreşim periyodunun T1>TB veya (ω1(1))2 ≤ ωB2 koşulunu sağlandığının gösterilmesi yeterlidir. Burada başlangıç eğimi olan (ω1(1))2 değeri binanın hakim doğal titreşim periyodu T1 'in TB 'den büyük olması anlamına gelmektedir. Bu durumda TBDY Denklem 5B.17a uygulanarak spektral yerdeğiştirme oranı CR=1 alınır ve d1,max(X) = Sde(T1) olarak hesaplanır.
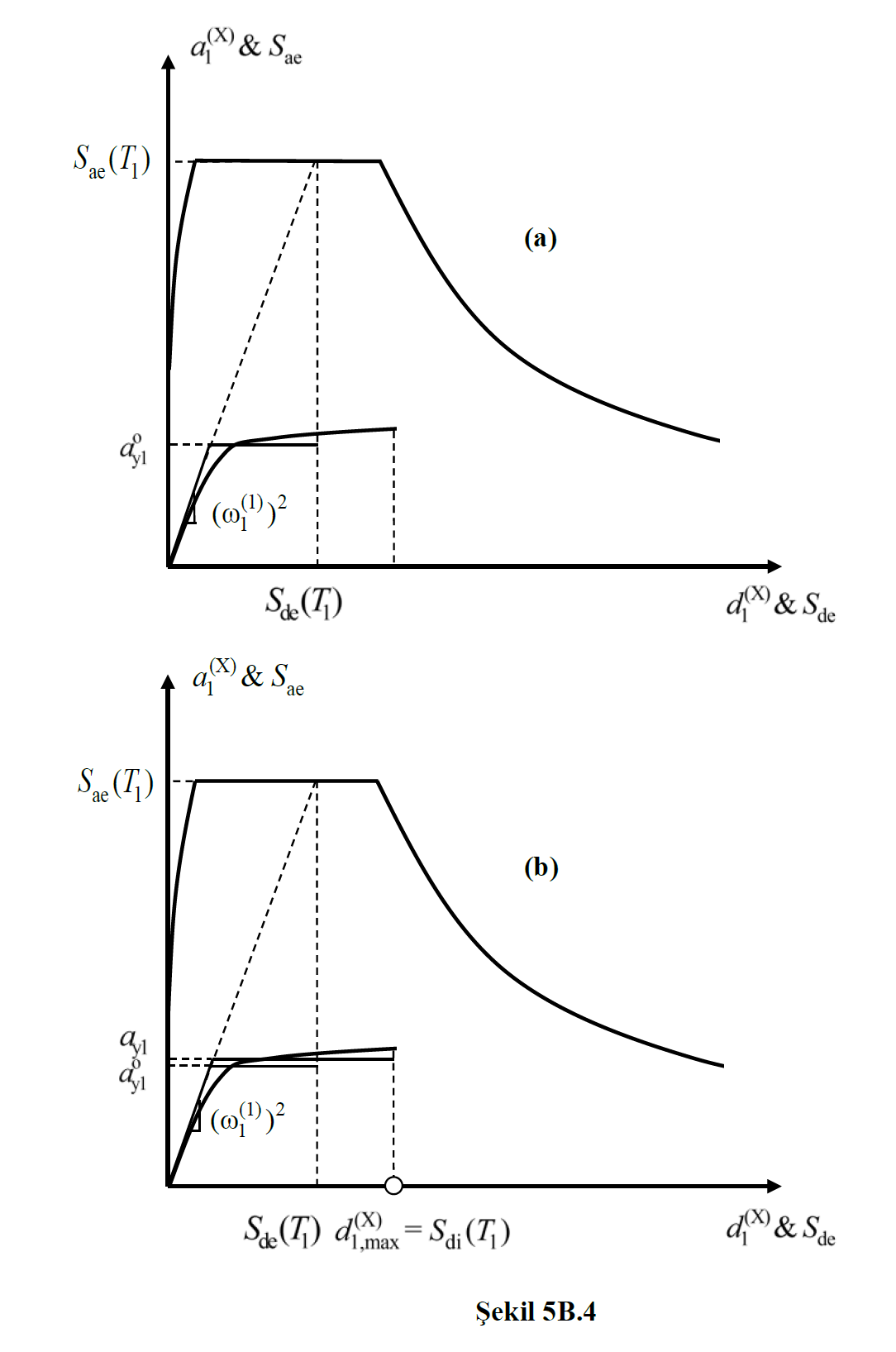
Öte yandan binanın hakim doğal titreşim periyodu T1 'in TB 'den küçük olması (Şekil 5B.4 ’te gösterilen durum), Denklem 5B.13 ile birlikte Denklem 5B.17b ’nin uygulanmasına karşı gelmektedir. Bu durumda spektral yerdeğiştirme oranı CR , ardışık yaklaşımla hesaplanır. Bu amaçla modal kapasite diyagramı, Şekil 5B.4a ’da gösterildiği üzere, önce CR =1 alınarak iki doğrulu elasto-plastik bir diyagrama dönüştürülür. Dönüşüm işleminde diyagramların altında kalan alanların eşitliği esas alınır. Bu şekilde bulunan yaklaşık akma sözde-ivmesi ay1o kullanılarak Denklem 5B.15 ’den Ry ve buna bağlı olarak Denklem 5B.17b ’den CR ve Denklem 5B.13 ’ten Sdi(T1) hesaplanır. Buna göre elasto-plastik diyagram tekrar oluşturulur (Şekil 5B.4b) ve yeniden bulunan ay1 esas alınarak aynı işlemler tekrarlanır. Sonuçların yeterince yaklaştıkları adımda ardışık yaklaşıma son verilir.
Sonraki Konu
