Yerdeğiştirmiş Eksen Dönmesi (15A.2)
Yerdeğiştirmiş eksen dönmesi değerleri doğrusal performans analizinde kolon, kiriş ve perde elemanlarında birim şekildeğiştime ve plastik dönme taleplerinin hesaplanması için kullanılır.
Yerdeğiştirmiş eksen dönmesi θk otomatik hesaplanır.
SİMGELER
I = Atalet momenti
Lp = Plastik mafsal boyu
lc = Eleman net açıklığı
Ra = Deprem Yükü Azaltma Katsayısı
UX = Üç boyutlu analiz modelinde düğüm noktasının ( X ) yönünde yaptığı öteleme
UY = Üç boyutlu analiz modelinde düğüm noktasının ( Y ) yönünde yaptığı öteleme
UZ = Üç boyutlu analiz modelinde düğüm noktasının ( Z ) yönünde yaptığı öteleme
RX = Üç boyutlu analiz modelinde düğüm noktasının ( X ) ekseni etrafında yaptığı dönme
RY = Üç boyutlu analiz modelinde düğüm noktasının ( Y ) ekseni etrafında yaptığı dönme
RZ = Üç boyutlu analiz modelinde düğüm noktasının ( Z ) ekseni etrafında yaptığı dönme
Δ = Eleman düğüm noktaları arası öteleme
ϕy = Akma eğriliği
ϕt = Toplam eğrilik
θp = Plastik dönme talebi
θy = Akma dönmesi
θyi = i ucundaki akma dönmesi
θyj = j ucundaki akma dönmesi
θk = Yerdeğiştirmiş eksen dönmesi
θki = i ucundaki yerdeğiştirmiş eksen dönmesi
Mevcut binaların Şekildeğiştirmeye Göre Değerlendirme ve Tasarım (ŞGDT) yaklaşımı ile deprem performansının belirlenmesinde doğrusal hesap yöntemi kullanılıyor ise eleman plastik dönme talebi θp veya eleman uç kesitinin eğrilik talebi ϕt doğrusal yöntemlerde hesaplanır.
Doğrusal performans analizi “bir elemandaki toplam şekildeğiştirme değeri o elemandaki elastik şekildeğiştirmeler ile plastik şekildeğiştirmelerin toplamına eşittir” prensibi ile yapılmaktadır. Sünek betonarme elemanlar için plastik şekildeğiştirmeler moment etkisinden ötürü oluşan dönme şekildeğiştirmeleridir. Bu yaklaşıma göre bir elemanın plastik şekildeğiştirme değerinin bulunması için o elemanın düğüm noktasın toplam şekildeğiştirme değeri bulunur ve sonra elastik şekildeğiştirmeler bu değerden çıkartılır.
Bir elemanın i ucunun plastik dönme talebi θp, aşağıdaki bağıntıdan hesaplanır.
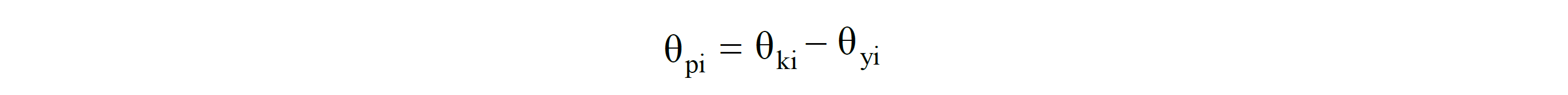
Benzer şekilde bir elemanın toplam eğrilik talebi ϕt, aşağıdaki bağıntıdan hesaplanır.
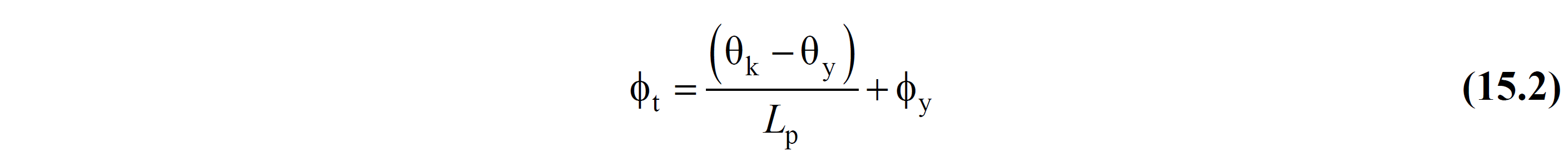
Bu bağıntılarda θki yerdeğiştirmiş eksen dönmesini ifade etmektedir ve Denk.(15A.1) 'den hesaplanır.
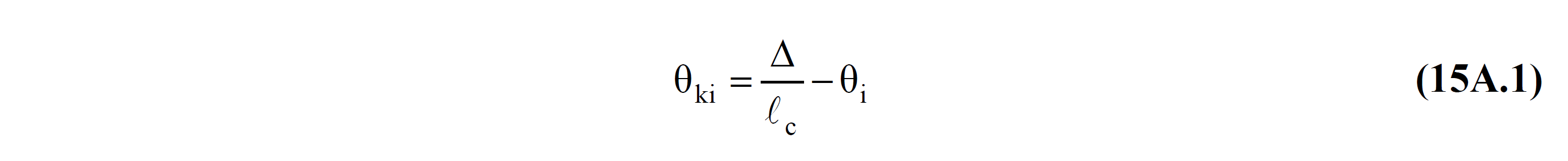
Bu denklemde Δ eleman uç düğüm noktaları arasındaki göreli ötelenmeyi temsil etmektedir. lc , eleman net açıklığıdır. θi değeri elemanın i düğüm noktasındaki düşey yükler ile Ra=1 olarak alınmış deprem yüklerinden (yükleme durumları) oluşan dönme değerini ifade eder. Bu durumda θki yalnızca doğrusal deprem hesabıyla yapılmış analiz sonuçlarından elde edilmektedir.
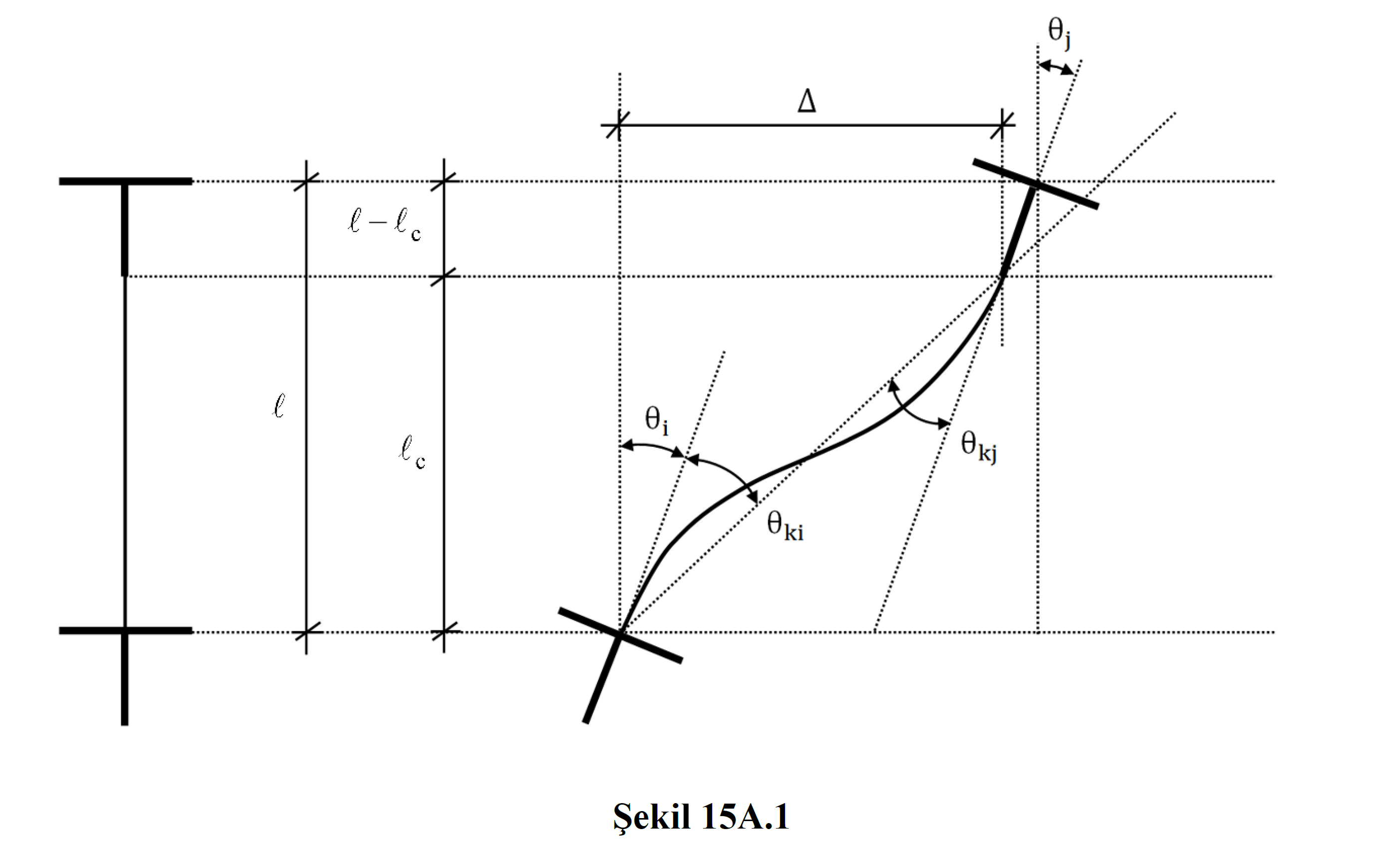
Kiriş elemanlarında kat arası ötelenme değeri sıfır olarak alınmaktadır ( Δ = 0 ).
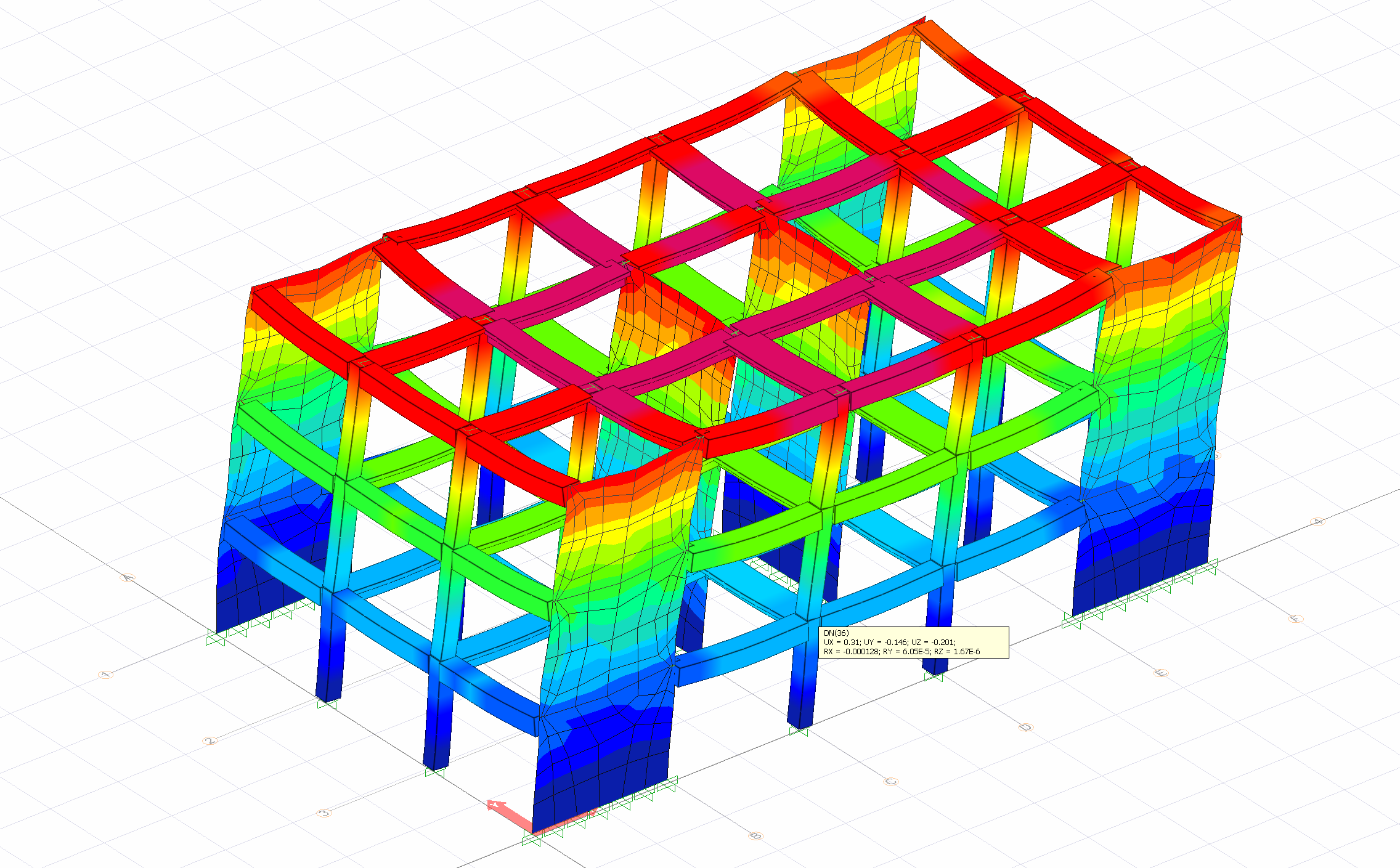
Yapı taşıyıcı sistem modeli üç boyutlu oluşturulduğundan eleman düğüm noktalarındaki göreli ötleme Δ değeri 'de üç boyutlu sistemde hesaplanır. Aşağıdaki resimde bir üç boyutlu bir analiz sisteminin herhangi bir eleman düğüm noktasındaki yerdeğiştirme sonuçları gösterilmiştir. Analiz sonuçlarında düşey yükler ile Ra=1 olarak alınmış deprem yüklerinden (yükleme durumları) oluşan düğüm noktası yerdeğiştirme değerleri kullanılır. Bu sonuçlar UX, UY ve UZ olmak üzere üç adet öteleme ile RX, RY ve RZ olmak üzere üç adet dönme değerleridir. Δ değeri hesaplanırken bütün kolon elemanlarının UX ve UY değerlerinin vektörel yerdeğiştirmeleri dikkate alınır. Benzer şekilde bir düğüm noktasının dönme değeri θki hesaplanırken RX ve RY dönme değerlerinin vektörel dönmeleri dikkate alınır.
Sonraki Konu
