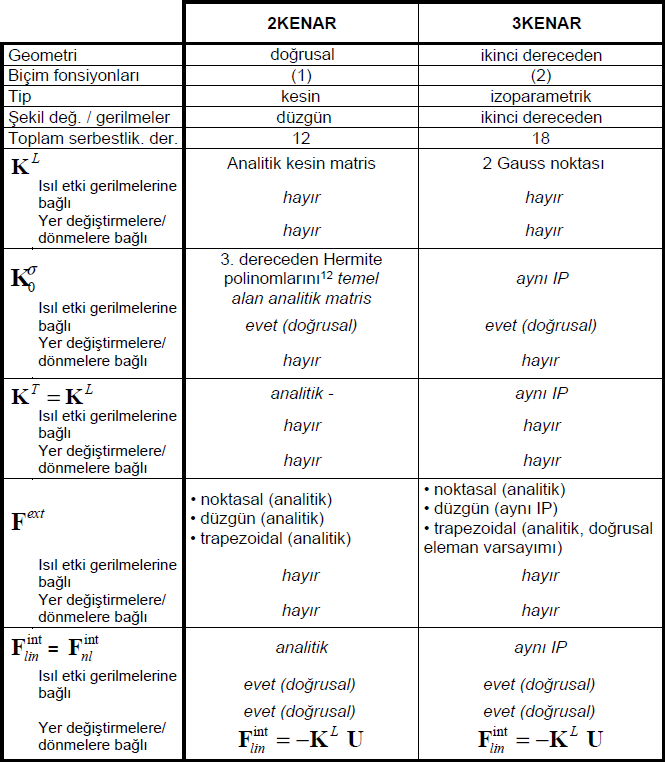
Doğrusal Kiriş Elemanlar

SİMGELER

v= Lokal vektör y'nin tanımlanması için "üçüncü-nokta" (3 değer)
E= Elastisite modülü
G= Kayma modülü (ön tanımlı olarak = E / 2(1+ ν ))
α = Isıl genleşme katsayısı
S_x= Eksenel rijitlik için kesit yüzeyi
S_y, S_z = İki etkin kayma kesiti yüzeyi (Bunlar, bir kesme düzeltme faktörü'nün⁸ dikkate alınabilmesi
için S_x'den farklı olabilirler.)
I_xx = Burulma ataleti
I_yy, I_zz⁹= Eğilme ataletleri
= Eksenel birim şekildeğiştirme
= Eğilme birim şekildeğiştirme
= Enine kayma birim şekildeğiştirme
= Burulma birim şekildeğiştirme

Mekanik Model

Bu doğrusal kiriş modelinde eksenel, enine-kayma, eğilme ve burulma rijitlikleri bulunmaktadır. Küçük-şekil
değiştirme/küçük-yer değiştirme esaslı Reissner-Timoshenko kiriş teorisini (doğrusal teori)⁷ temel
almaktadır. Bu teoride, malzeme kesit yüzeyleri sadece dönme yaparak şekil değiştirme yapmadan düzlem
kalmakta ve iki doğrultuda enine-kayma şekil değiştirmesine izin verilmektedir (kesit yüzeyi ile ortalama
orta eksen arasındaki açı değişebilmektedir = kalın-kiriş teorisi) [BAT]. Bu model, ince-cidarlı kiriş
modellerindeki gibi (Vlassov teorisi gibi) kesit yüzeyinin çarpılmasını dikkate almaz. Bünye denklemlerinin
doğrusal elastik olması gerekmektedir (Hooke yasası). En az 12 skaler parametresi bulunur.

Ek olarak, dönüşüm atalet aksları olan ve tarafsız ekseni sonlu eleman çizgisinden kaydırmak amacıyla y₀
ve z₀ şeklinde tarafsız kaçıklıkları bulunan kirişler için I_yz şeklinde bir dönüşüm ataleti tanımlanabilir.
Yasa ayrıca tek tek eleman esaslı bir temel üzerinden de tanımlanabilir. Bu durumda (değişken kesitli
kirişler), elemanların her bir ucu için bir geometrik değerler seti (S_x, S_y, S_z, I_xx, I_yy, I_zz, I_xy, y₀, z₀) tarif edilebilir.

x, y, z akslarının tanımı aşağıdaki şekildedir:
x , tanjant sonlu eleman çizgisi üzerindeki birim vektördür.
z, normalize yapılmış dönüşüm sonucu olan ile tanımlanır (eğer x ve v aynı doğru üstündeyse,
z isteğe göre seçilir).
Bunu takiben y = z × u ile dönüşüm sonucu elde edilir.

Kinematik, Şekil Değiştirmeler ve Gerilmeler

Bu elemanların her noktada altı serbestlik derecesi bulunmaktadır (global eksen bazlı 3 yer değiştirme ve 3 dönme).
Tüm şekil değiştirme ve gerilme terimlerinin kesit boyunca doğrusal değiştiği varsayılır. Sabit bir bölüm (membran ve kayma terimleri) ve merkezinde boş değer olan iki doğrusal değişken bölüme (eğilme ve burulma terimleri) ayrıştırılırlar.

Kesitlerde düzlem içi gerilmenin sıfır olması kabulü sebebiyle (σ_yy, σ_zz, σ_yz), makaslama enerjisi de sıfır olacaktır ve kesit şekil değiştirmeleri ihmal edilebilir (ε_yy, ε_zz, ε_yz değerleri 0 olur).
Sonuç gerilmeler aslında bileşke gerilmelerdir (kesit boyunca entegre edilmiş).
Bileşke gerilmeler¹⁰ şu şekildedir:

Hooke yasası ile bu denklemler şu şekilde yazılır¹¹:

Bu bileşke gerilmeler aslında iki adet 3-bileşenli vektör şeklinde olan sonuçlardır: kuvvet vektörü F (N ve Q)
ve moment vektörü M (M ve T). Lokal ya da global eksen bazlı olarak tarif edilebilirler. Kural şudur ki;
eğrisel bir x koordinatı için F(x) kuvveti ve M(x) momentumu, s ≥ x olan herhangi bir koordinat için kuvvet ve
momentum toplamlarına eşittir.

Doğrusal kirişler için özel bir ard-işlemci, gerçek şekil değiştirmeler ile birlikte her elemanın F(x) and M(x) diyagramlarını doğru şekilde sunmaktadır. Bu işlem kirişin doğrusal düz ve değişken kesitli olmamasını gerektirmektedir.

Geometri

Elemanların geometrisi için herhangi bir özel gereksinim bulunmamaktadır. Kiriş elemanları üç boyutlu tam
koordinatlara sahiptir. Sonlu eleman ağları ve elemanlar (3KENARLI) eğrisel olabilir.

Yükler

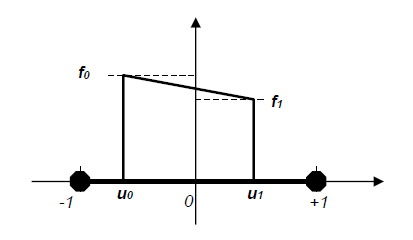
Mekanik yükler, noktasal (KUVVET ve MOMENTUM), düzgün yayılı (sadece KUVVET) ya da trapezoidal yayılı (sadece KUVVET) olabilir. Trapezoidal yayılı yük, iki parametre yükün tanım alanı için (-1 ≤ u₀ < u₁ ≤ +1) ve iki katsayı da yük değeri için (yük vektörü üzerindeki f₀ ve f₁ çarpımsal katsayıları) olmak üzere toplam dört terim ile tanımlanmaktadır.

Eşdeğer noktasal yükler dahili olarak çözümlenmekte ve bu sayede nihai sonlu eleman çözümü hatasız olmaktadır. Isı yükleri, her elemanda düzgün yayılı ve her iki kesit doğrultusunda doğrusal olacak şekildedir (iki ısıl eğilme momenti oluşturacak şekilde).

Notlar

2KENAR kiriş elemanı, gerçek U ile R değerleriyle ve gerçek bileşke gerilmelerle, doğrusal düzgün kesitli ve doğrusal değişken kesitli kirişler (doğrusal değişen kesitli ve ataletli) için noktasal, düzgün yayılı ve trapezoidal yayılı yüklerle birlikte hatasızdır. Rijitlik matrisi herhangi bir sayısal entegrasyon olmadan analitik olarak çözümlenir. Ancak, ataleti ikinci ya da daha yüksek mertebenden polinomlarla ifade edilen kirişler için, sonlu elemanlar çözümü sadece yaklaşık olarak tahmin edilebilir (kesin sonuçtan çok az daha rijit), ve yakınsaması için sonlu eleman ağı sıklaştırılmalıdır.
2KENAR modeli eğrisel tanımlar için tam olarak doğru değildir. Sonlu eleman ağı oluşturulmalıdır.
3KENAR kiriş eleman ile hesaplanan U ve R tanım alanları sadece iki uçta kesindir – orta noktada kesin değil – ve sadece düzgün yayılı ya da noktasal yük etkisindeki düzgün doğrusal kiriş özel durumu için geçerlidir. Bu eleman, sadece arklar, yayılı yaylar üzerine oturan kirişler ya da kabuk destekleyici kirişler için 2-noktalı kenar elemandan daha uygun olabilir.
Kayma kaçıklığı yoktur (kayma merkezinin tarafsız eksene göre kaçıklığı).
Kiriş elemanın kütlesi ya da sönüm değeri yoktur sadece rijitliği bulunur. Dinamik bir analiz için, rijitlik
modeline ek olarak ayrıca bir kiriş kütle ya da bir çizgisel kütle modeli kullanılmalıdır.

2KENAR elemanı için lokal matris olan , Oxyz (değişken olmayan durumda) lokal eksen bazı içinde
aşağıda sıralanmış serbestlik dereceleri ile oluşturulur:

Ux0, Uy0, Uz0, Rx0, Ry0, Rz0, Ux1, Uy1, Uz1, Rx1, Ry1, Rz1

ile:

Bu matris daha sonra global serbestlik dereceleri koordinatlarına dönüştürülür:

Burada T, lokal eksen bazının globala çeviriminden olan dönüşüm matrisidir.

T matrisi, eksenel kuvvet ile eğilme momentumları arasından bir etkileşime yol açan kaçıklıkları da arıca
dikkate almaktadır.

⁷ Büyük-şekil değiştirme/büyük-yer değiştirme teorisine dayanan geometrik rijitlik matrisi hariç.
⁸ Enine-kayma etkisini (ince-kiriş teorisi) ihmal etmek için etkin kayma yüzeyleri, örnek olarak 1000 S_x gibi büyük bir
değere ayarlanabilir. Değeri sıfır yapmak, 2-noktalı kiriş elemanı ile aynı etkiye sahiptir.
⁹ Ataletler aşağıdaki şekilde tanımlanmıştır:

Burada I_yy , z etrafında dönme için atalet ve I_zz de y etrafında dönme için olan ataletlerdir.

¹⁰ Not edilmelidir ki, bu tanımlarla, y ekseni etrafındaki eğilme momenti M_z ve z ekseni etrafındaki de –M_y 'dir.

¹¹ Burada atalet eksenlerinin lokal eksenlerle uyumlu olduğu (atalet dönmesi olmadan) ve tarafsız çizgide herhangi bir kayma olmadığı kabul edilir. Eğer bu şekilde değilse, membran ile eğilme ve kayma ile burulma arasından bir eşleştirme dikkate alınır.

¹² Sadece eksenel gerilme etkisi için analitik. Eğilme, kayma ve burulma gerilmeleri etkileri için düzgün integrasyon.

Sonraki Konu

Doğrusal Olmayan Kiriş Elemanlar

İlgili Konular