Poligon Perdelerin Tasarım Eğilme Momentleri Hesabı
Hw / lw > 2.0 koşulunu sağlayan perdelerde tasarıma esas eğilme momentleri, 7.6.2.2’ye göre belirlenen kritik perde yüksekliği boyunca sabit bir değer olarak, perde tabanında Bölüm 4’e göre hesaplanan eğilme momentine eşit alınır koşulu otomatik kontrol edilir.
Kritik perde yüksekliğinin sona erdiği kesitin üstünde ise, Bölüm 4 ’e göre perdenin tabanında ve tepesinde hesaplanan momentleri birleştiren doğruya paralel olan doğrusal moment diyagramı otomatik uygulanır.
3.3.1.1’de verilen koşulları sağlayan bodrumlu binalarda sabit perde momenti, 7.6.2.2’de tanımlanan kritik perde yüksekliği boyunca gözönüne alınır.
Hw / lw ≤ 2.0 olan perdelerin bütün kesitlerinde tasarım eğilme momentleri, Bölüm 4’e göre hesaplanan eğilme momentlerine eşit alınması koşulu otomatik uygulanır.
Hw / lw > 2.0 olması durumunda, her bir katta perde kesitlerinin taşıma gücü momentlerinin, perdenin güçlü doğrultusunda kolonlar için Denk.(7.3) ile verilen koşulun sağlayıp sağlanmadığı otomatik kontrol edilir.
SİMGELER
Hw = Temel üstünden veya zemin kat döşemesinden itibaren ölçülen toplam perde yüksekliği
Hcr = Perde kritik yüksekliği
lw = Perdenin veya bağ kirişli perde parçasının plandaki uzunluğu
Poligon Perde Hw / lw > 2 ve Hw / lw <= 2 Koşullarında Tasarım Eğilme Momentleri
Poligon perde elemanları kabuk sonlu elemanlar ile modellenmektedir. Bu durumda her bir yükleme kombinasyonunda perde elemanının gerilmeleri hesaplanmaktadır. Poligon perde sonlu elemanlarının sonuçları üç boyutlu rijit cisim hareketi koşulunu sağlayacak şekilde poligon perde kesiti ağırlık merkezinde tanımlanır ve İlgili yükleme kombinasyonunun perde sonlu eleman sonuçlarından elde edilen değerler bu ağırlık merkezinde toplanarak poligon perdenin iç kuvvetleri elde edilir.
Poligon perde elemanlarının, TBDY Bölüm 7.6 gereğince önce minimum boyuna donatısı ve enine donatısı belirlenmektedir. Bu donatılarla elde edilen eleman dayanımları, hesaptan elde edilen tasarım kuvvetleriyle karşılaştırılmaktadır. Dayanım değerlerinin tasarım kuvvetlerinden daha küçük olması durumunda öngörülen donatılar revize edilerek gerekli eleman dayanımı elde edilmektedir.
Bütün yükleme durumları poligon perdenin sonlu elemanlarında gerilmeler meydana getirir. Bu sonlu eleman sonuçları poligon perdenin ağırlık merkezinde üç boyutlu rijit cisim hareketini sağlayacak şekilde toplandığında poligon perdede eksenel yük ile birlikte her iki eksen etrafında eğilme momenti meydana getirir. Bu durumda poligon perdenin iki ekseninde (kuvvetli ve zayıf ekseninde) her bir normal kuvvet seviyesi için bir eğilme dayanımı hesaplanır. Tüm bu dayanımlar PM2M3 şeklinde bir grafiğe taşındığında perdenin 3 boyutlu etkileşim eğrisi elde edilir. Perdelerde eğilme dayanımı her bir yükleme kombinasyonu için farklı normal kuvvet seviyesi olacağından moment-eğrilik analizi ile hesaplanmaktadır. Her normal kuvvet seviyesinde hesaplanan moment dayanımı poligon perdenin 3 boyutlu etkileşim eğrisini oluşturur. Poligon perdenin tamamında moment eğrilik analizi yapılırken başlık bölgelerinde ve diğer bölgelerdeki boyuna donatılar kendi konumlarında olmak üzere kesit hücresi (lif veya fiber) modeli kullanılır.
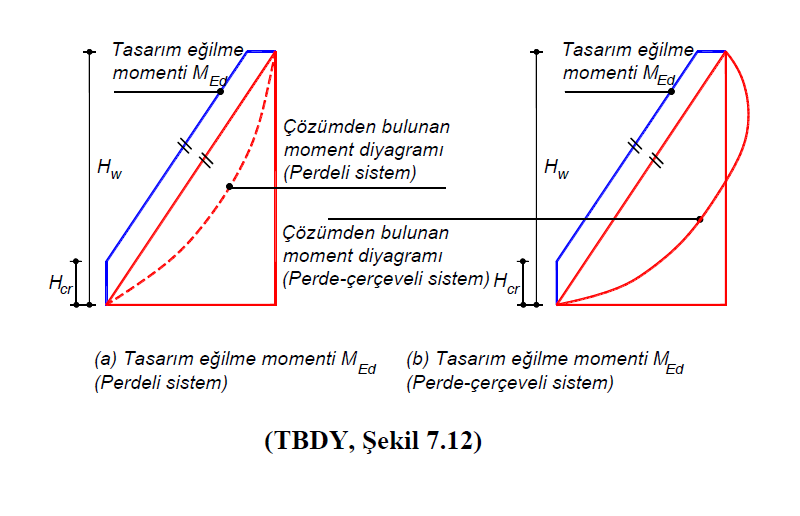
TBDY Madde 7.6.6.1 'e göre Hw / lw > 2 olan poligon perdelerin tasarım eğilme momentleri TBDY Şekil 7.12(a) ve TBDY Şekil 7.12(b) 'de gösterilen kritik perde yüksekliği, Hcr , boyunca sabit bir değer, kritik perde yüksekliğinin sona erdiği kesitin üstünde ise poligon perdenin tabanında ve tepesinde hesaplanan momentleri birleştiren doğruya paralel olan moment diyagramının değerleridir. Hw / lw > 2 koşulunu sağlayan perdelerde tasarıma esas eğilme momentleri, doğrusal elastik şekil değiştirmeler perde kritik yüksekliği, Hcr, boyunca beklenir. Bu nedenle Hcr boyunca perdenin taban momentine eşit sabit bir değer olarak tasarlanmaktadır.
TBDY Madde 7.6.6.1 'e göre Hw / lw > 2 koşulunu sağlayan poligon perdelerde tasarım eğilme momentleri, TBDY Madde 7.6.2.2 'ye göre belirlenen kritik perde yüksekliği boyunca sabit bir değer olarak poligon perde tabanında Bölüm 4 'e göre hesaplanan eğilme momentine eşit alınmaktadır. Poligon perdenin taban momenti düşey yükler ve deprem yüklerinin ortak etkisi altında hesaplanan eğilme momenti değeridir. Bu eğilme momenti kritik perde yüksekliği, Hcr , boyunca sabit bir şekilde devam etmektedir.
TBDY Şekil 7.12(a) ve TBDY Şekil 7.12(b) 'de söz edilen “Çözümden bulunan moment diyagramı” her iki sistem (perdeli , perde-çerçeveli) için düşey yükler ve deprem yüklerinin ortak etkisi altında oluşan moment diyagramını temsil etmektedir. “Tasarım eğilme momenti MEd“ ile gösterilen grafik (mavi renk) kritik perde yüksekliği, Hcr , boyunca perdenin tabanında bulunan moment ile aynı değerdeki moment diyagramıdır. Kritik perde yüksekliği, Hcr , değerinin üst kısmında ise perdenin taban momenti ile tavan momentini birleştiren çizgiye paralel olan moment diyagramıdır. Bu moment diyagramı poligon perdenin eğilme tasarımında kullanılacak olan moment diyagramıdır. Perde yüksekliği boyunca tasarım eğilme momenti diyagramı çizildikten sonra her bir poligon perde kesitinde tasarım eğilme momenti değerinin eğilme dayanımından büyük olup olmadığı kontrol edilir. Bu hesapta normal kuvvet ile beraber iki eksenli moment etkileşimi dikkate alınmaktadır.
Poligon perdelerde Tasarım Eğilme Momenti grafiği taban momentine bağlı olduğundan tüm kombinasyonlar için ayrı ayrı yapılmaktadır. Diğer bir deyişle perdelerde tüm kombinasyonlar için tasarım eğilme momenti değeri ayrı ayrı hesaplanmaktadır. Poligon perdelerde Tasarım Eğilme Momenti diyagramı iki eksen için de (kuvvetli ve zayıf eksen) hesaplanmaktadır. Perde enkesitleri I, T, L, U, C veya daha farklı şekilde olduğundan eğilme davranışında iki yönün de dikkate alınması gerekmektedir. Bu nedenle poligon perdelerde tasarım eğilme momenti değeri bütün kombinasyonlar için iki eksen (kuvvetli ve zayıf eksen) için de hesaplanmaktadır. Daha sonra her normal kuvvet seviyesi için bir eğilme dayanımının hesaplandığı 3 boyutlu etkileşim eğrisi (soğan eğrisi) çizilir. Bu değerlerden sonra perdenin tasarım oranları her kombinasyon için bulunur.
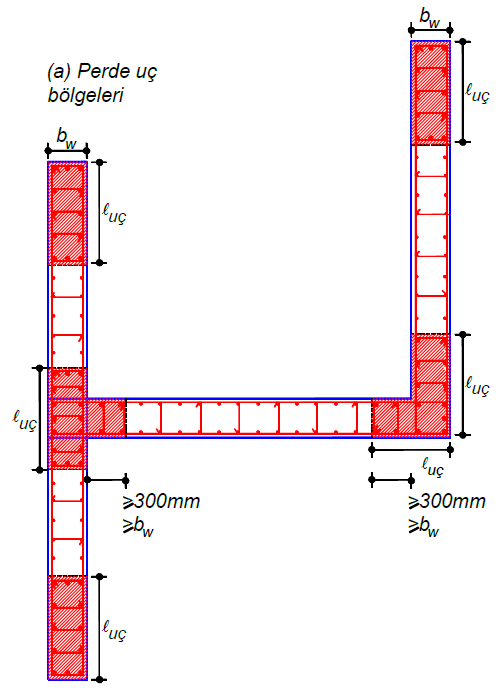
Aşağıdaki resimde bir poligon perde örneği gösterilmiştir.
Sonraki Konu
