Yapı Modal Karakteristikleri ve Deprem Yükü Artımlarının Belirlenmesi (5B.1.1)
Modal Karakteristikler, TBDY EK 4B 'de verilen Modal Katkı Çarpanı, Taban Kesme Modal Etkin Kütlesi ve Mod Şekli otomatik hesaplanır.
SİMGELER
a1(X,k) = (X) deprem doğrultusu için k’ıncı itme adımında birinci moda ait modal tek serbestlik dereceli sistem’in modal sözde-ivmesi [m/s2]
mi = i 'nci katını toplam kütlesi
mix1(X,1) = (X) deprem doğrultusu için x ekseni doğrultusunda birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’ne göre hesaplanan i’inci kat modal etkin kütlesi [t]
mtx1(X,1) = (X) deprem doğrultusu için x ekseni doğrultusunda birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’ne göre hesaplanan taban kesme kuvveti modal etkin kütlesi [t]
miy1(X,1) = (X) deprem doğrultusu için y ekseni doğrultusunda birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’ne göre hesaplanan i’inci kat modal etkin kütlesi [t]
miθ1(X,1) = (X) deprem doğrultusu için z ekseni etrafında birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’ne göre hesaplanan i’inci kat modal etkin kütle eylemsizlik momenti [tm2]
Δa1(X,k) = (X) deprem doğrultusu için k’ıncı itme adımında birinci moda ait modal tek serbestlik dereceli sistem ’in modal sözde-ivme artımı [m/s2]
Δfix1(X,k) = (X) deprem doğrultusu için k ’ıncı itme adımında i ’inci katta x ekseni doğrultusunda etkiyen deprem yükü artımı [kN]
Δfiy1(X,k) = (X) deprem doğrultusu için k ’ıncı itme adımında i ’inci katta y ekseni doğrultusunda etkiyen deprem yükü artımı [kN]
Δfiθ1(X,k) = (X) deprem doğrultusu için k ’ıncı itme adımında i ’inci katta z ekseni doğrultusunda etkiyen deprem yükü artımı [kN]
Φix1(1) = i’inci katta birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’nin x doğrultusundaki genliği
Φiy1(1) = i’inci katta birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’nin y doğrultusundaki genliği
Φiθ1(1) = i’inci katta birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’nin z ekseni etrafındaki dönme genliği
Γ1(X,1) = (X) deprem doğrultusu için birinci itme adımında belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ’ne göre hesaplanan modal katkı çarpanı
Sabit Tek Modlu İtme Yöntemi, gözönüne alınan deprem doğrultusunda her bir itme adımında katlara etkiyen deprem yükü artımları, başlangıç adımında, deprem dışı yüklemeler altında doğrusal olmayan artımsa statik hesap (0 'ıncı adım) 'tan sonraki birinci adımda belirlenen ve itme hesabı boyunca hiç değiştirilmeyen sabit mod şekli ile orantılı olarak tanımlanır. İtme analizi sonucunda koordinatları taban kesme kuvveti-tepe yerdeğiştirmesi olan itme eğrisi elde edilir. Daha sonra bu eğriye koordinat döşümü uygulanarak koordinatları modal yerdeğiştirme-modal sözde ivme olan modal kapasite diyagramı elde edilir. Moda kapasite diyagramı kullanılarak elde edilen performans noktası sonucunda, bu performans noktasındaki plastik şekildeğiştirmeler ve iç kuvvetler sınır değerler ile karşılaştırılarak bina performansı belirlenir.
TBDY EK 5B.1.1 'de belirtildiği üzere, Sabit Tek Modlu İtme Yöntemi 'nde, deprem dışı yüklemelerden oluşan ikinci mertebe etkilerinin gözönüne alındığı iç kuvvetler ve şekildeğiştirmeler başlangıç değeri olarak (0 'ıncı adım) dikkate alınır. Gözönüne alınan deprem doğrultusundaki k 'ıncı İtme adımında katlara etkiyen deprem yükü artımları, deprem dışı yüklemelerden sonraki birinci adımda modal hesap yöntemleri ile hesaplanan mod şekli ve kat modal etkin kütleleri cinsinden Denklem 5B.1 ile ifade edilir.
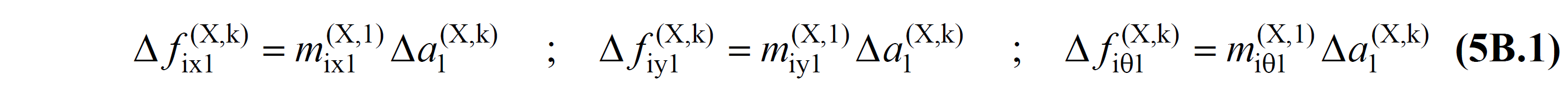
Burada Δfix1(X,k) , Δfiy1(X,k) ve Δfiθ1(X,k) terimleri, gözönüne alınan ( X ) deprem doğrultusu için k 'ıncı itme adımında katlara etkiyen deprem yükü artımlarıdır. mix1(X,1) , mix1(X,1) ve miθ1(X,1) terimleri kat etkin kütlelerinin birinci adımda hesaplanan birinci mod (hakim mod) karşılığıdır ve Denklem 5B.2 kullanılarak hesaplanır.
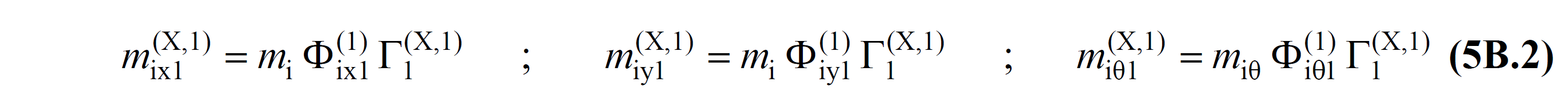
Denklem 5B.2 'de Φix1(1) , Φiy1(1) ve Φiθ1(1) terimleri deprem dışı yüklemelerden oluşan ikinci mertebe etkileri gözönüne alınan başlangıç adımında, şekildeğiştirmiş sistemin modal analizi yapılarak elde edilen birinci (hakim) mod şeklidir. Bu mod şeklinin sırasıyla x,y,z eksenlerindeki karşılıkları olarak ifade edilir. Aynı denklemde Γ1(X,1) değeri de başlangıç adımında yapılan modal analiz sonucunda elde edilen modal katkı çarpanıdır.
Denklem 5B.2 'de mi i 'nci katın toplam kütlesi, miθ i 'nci katın kütle eylemsizlik momenti olarak ifade edilir ve Tekil Düğüm Noktaları Kütleleri Tanımlanması (5.4.6) başlığında anlatıldığı şekli ile modellenir.
Φix1(1) , Φiy1(1) , Φiθ1(1) ve Γ1(X,1) değerleri yapı modal karakteristik değerlerini oluşturur. Bu değerler ikinci mertebe etkileri gözönüne alındığı şekildeğiştirmiş sisteme modal analiz uygulanarak elde edilir ve bütün itme adımlarında hakim modun yapısal karşılıları kullanılır. TBDY EK 4B 'te tanımlanan yapısal karşılıkları detaylı anlatımı Mod Birleştirme Yöntemiyle En Büyük Davranış Büyüklükleri Hesabı (4.8.2.1) başlığı altında bulunmaktadır.
Ardışık iki mafsal mafsal oluşumu arasında tanımlanan k 'ıncı itme adımında bilinmeyen büyüklük, birinci moda ait modal tek sertbestlik dereceli sistem 'in Denk.(5B.1) 'de yer alan modal sözde ivme artımı Δa1(X,k) 'dır ve detaylı açıklaması Modal Sözde İvme ve Modal Yerdeğiştirmenin Hesaplanması (5B.1.2 , 5B.1.3) başlığında bulunmaktadır.
