Plastik Mafsal Modeli (5.3.1)
Çubuk sonlu elemanlar olarak modellenebilen kolon ve kirişlerde doğrusal olmayan davranış modeli Yığılı Plastik Davranış (Plastik Mafsal) Modeli kullanılır ve plastik mafsallar plastik şekildeğiştirme bölgesinin ortasında otomatik olarak tanımlanır.
Plastik mafsal boyu kesit yüksekliğinin yarısı olacak şekilde otomatik hesaplanır.
Plastik mafsal kesitlerinde TBDY EK 5A 'da belirtilen beton ve donatı malzeme modelleri kullanılır. Yeni yapılacak veya mevcut binaların analizinde sargılı-sargısız beton ve donatı modeli otomatik oluşturulur.
Plastik mafsal iskelet eğrisi fiber model kullanılarak yapılan moment-eğrilik analizi ile otomatik oluşturulur.
Etkin akma momenti hesabında eksenel kuvvet ve iki eksenli eğilme etkisinden meydana gelen etkiler otomatik hesaplanır.
Elemanlarda fiber model çözümü otomatik olarak yapılır.
SİMGELER
h = Kesit yüksekliği
Lp = Plastik mafsal boyu
My = Etkin akma momenti
Mu = Göçme momenti, güç tükenmesi momenti
Mp = Plastik moment
εc = Betonun birim şekildeğiştirme değeri
ϕ = Eğrilik
ϕy = Akma eğriliği
ϕu = Göçme öncesi eğrilik, güç tükenmesi eğriliği
ϕp = Plastik eğrilik istemi, ϕp = ϕu - ϕy
θ = Yerdeğiştirmiş eksen dönmesi
θp = Plastik dönme istemi, kesitin yapabileceği en büyük plastik dönme
Yığılı Plastik Davranış Modeli, doğrusal olmayan eğilme şekildeğiştirmelerin küçük bir bölgede plastik mafsal adı verilen belirli bir bölgede toplandığı varsayımı ile oluşturulan davranış modelidir. Plastik mafsal bölgesi dışında kalan bölgelerde ise sistemin doğrusal-elastik davrandığı varsayılmaktadır. Plastik mafsalın meydana gelebilmesi için, bu bölgedeki kesitlerin plastik eğrilik kapasitesine sahip olması gerekir. Ayrıca, bu kapasitenin kullanılabilmesi, ortaya çıkan plastik şekil değiştirmelerin kabul edilebilir seviyede kalması gerekir.
Doğrusal olmayan şekildeğiştirmeler, çubuk eleman üzerinde plastik mafsal boyu, Lp uzunluğundaki bir bölgeye yayılmaktadır. TBDY Madde 5.3.1.2 'de belirtildiği üzere Plastik mafsal boyu olarak adlandırılan plastik şekildeğiştirme bölgesi ’nin uzunluğu (Lp), kesit yüksekliği (h) 'nin yarısı olarak hesaplanmaktadır (Lp = 0.5h). TBDY Madde 5.3.1.4 'e göre plastik mafsal, plastik şekildeğiştirme bölgesi 'nin ortasına yerleştirilmedir. Bu durumda plastik mafsal tanımlanan elemanların temiz açıklığındaki uçlarından Lp/2 kadarlık bir mesafede tanımlanır. Aşağıdaki şekilde betonarme kolon-kiriş birleşim bölgesinde kirişlerde oluşan plastik mafsal boyu gösterilmiştir. Yığılı Plastik Davranış Modeli 'ne göre Plastik şekildeğiştirmeler 'in Lp uzunluğu boyunca olduğu kabul edilmekte ve plastik mafsal Lp uzunluğunun yarısına yerleştirilmektedir.
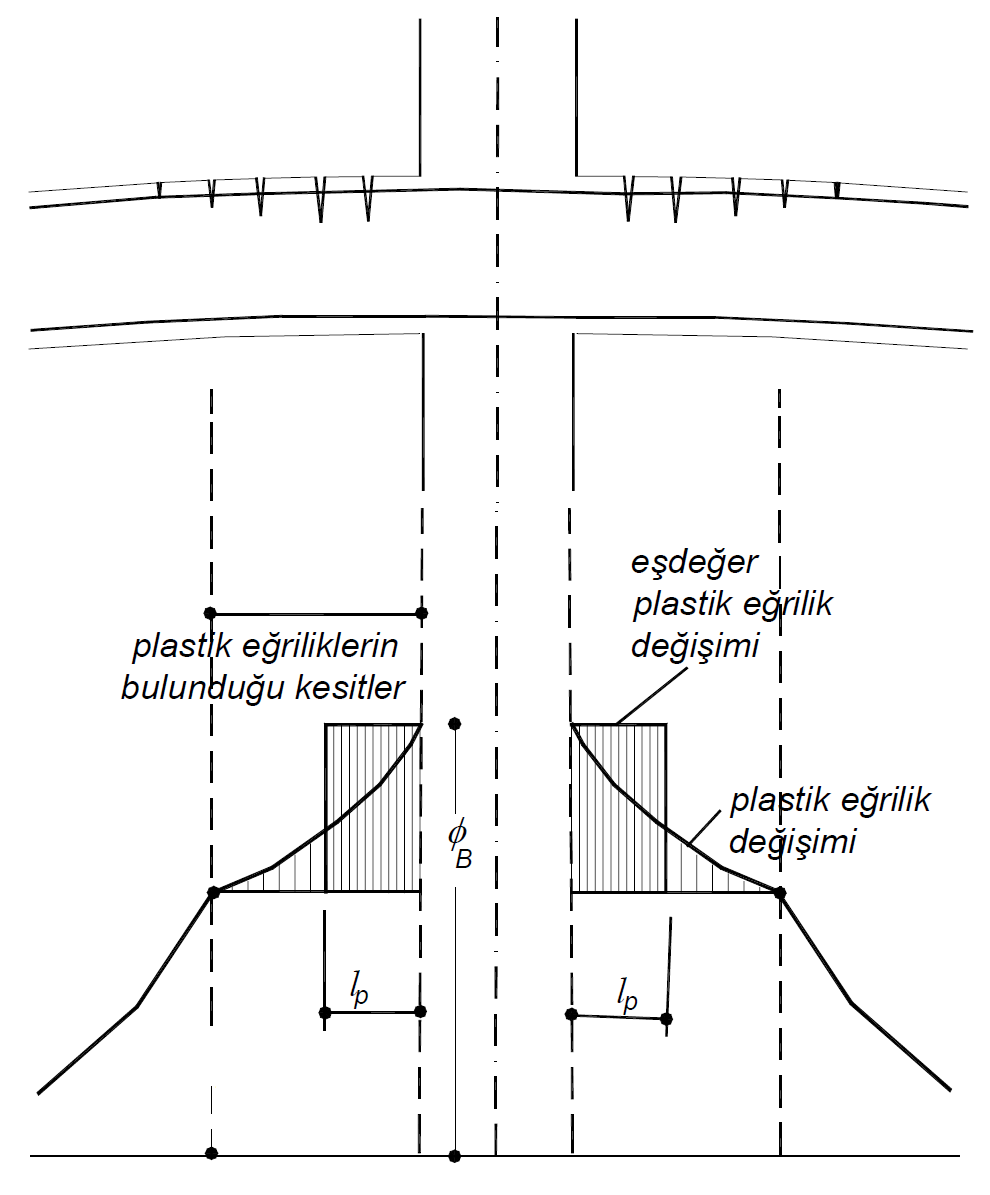
Plastik mafsallar elemanların plastik şekildeğiştirmeleri 'ni temsil etmektedir. Bu nedenle plastik mafsal tanımı yapılırken betonarme kesitlerin moment-eğrilik ilişkisinden yararlanılmaktadır. Moment-eğrilik ilişkisinde kesit davranışının sünekliği, farklı moment düzeylerinde kesit rijitliğinin değişimi, kullanılan malzeme modeline göre kabuk ve çekirdek betonunda ezilmenin oluşup oluşmadığı, kesitte sargılı beton etkisini, eğilme donatısının kopup kopmadığı, eğilme donatısının pekleşmesinin davranış üzerine etkisi gözlemlenebilir. Eğrilik, kesitteki şekildeğiştirmeyi belirten geometrik bir değişkendir.
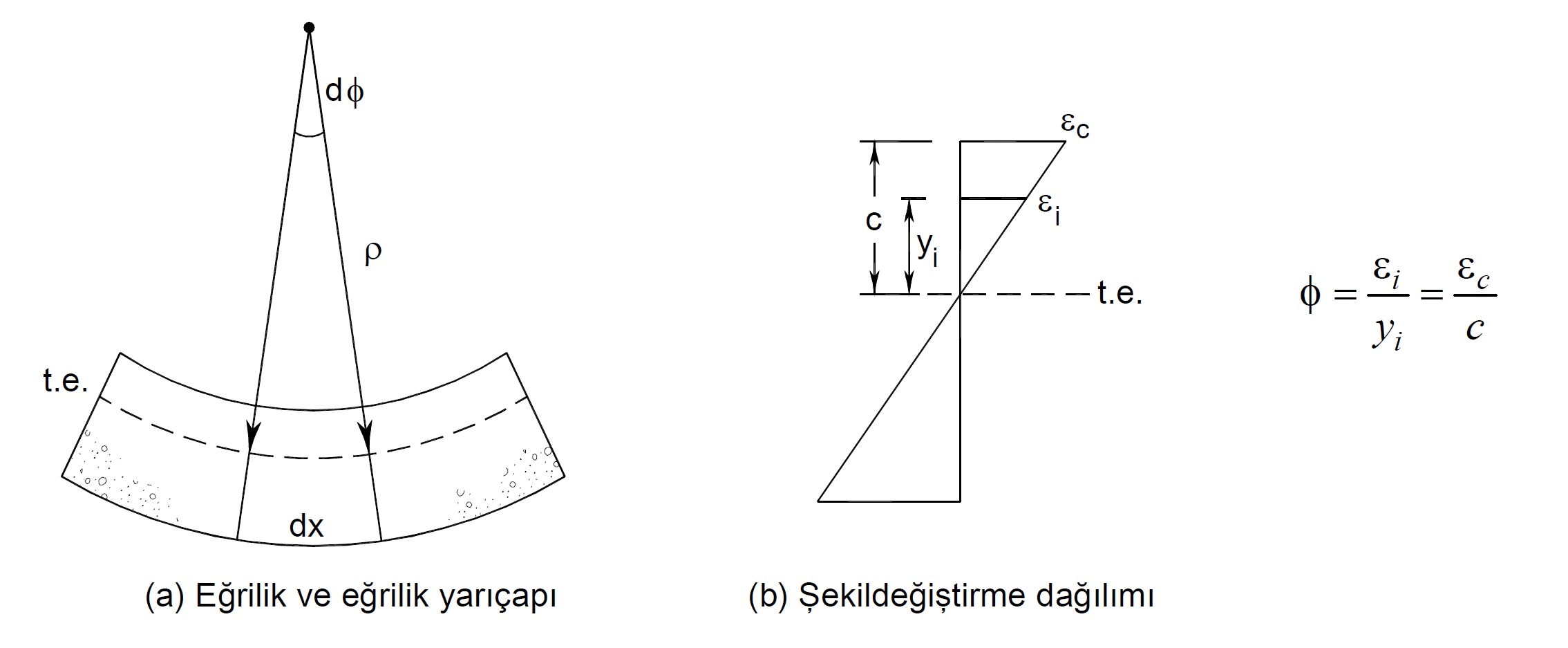
Yukarıdaki şekilde eğilme ve eksenel kuvvet etkisi altında şekildeğiştirmiş bir eleman parçası ve basit moment eğrilik ilişkisi gösterilmektedir. Moment eğrilik ilişkisinde tanımlanan beton donatı malzeme modellerine göre her bir moment değeri sonucunda ortaya çıkan şekildeğiştirme dağılımında, betonun birim şekildeğiştirme değerini, εc tarafsız eksen yüksekliği, c değerine bölünmesi ile eğrilik değeri elde edilir. Yukarıdaki resimde bulunan şekildeğiştirme dağılımı gösterilen bir kesitte eğrilik iki düzlem arasında kalan açıdır.
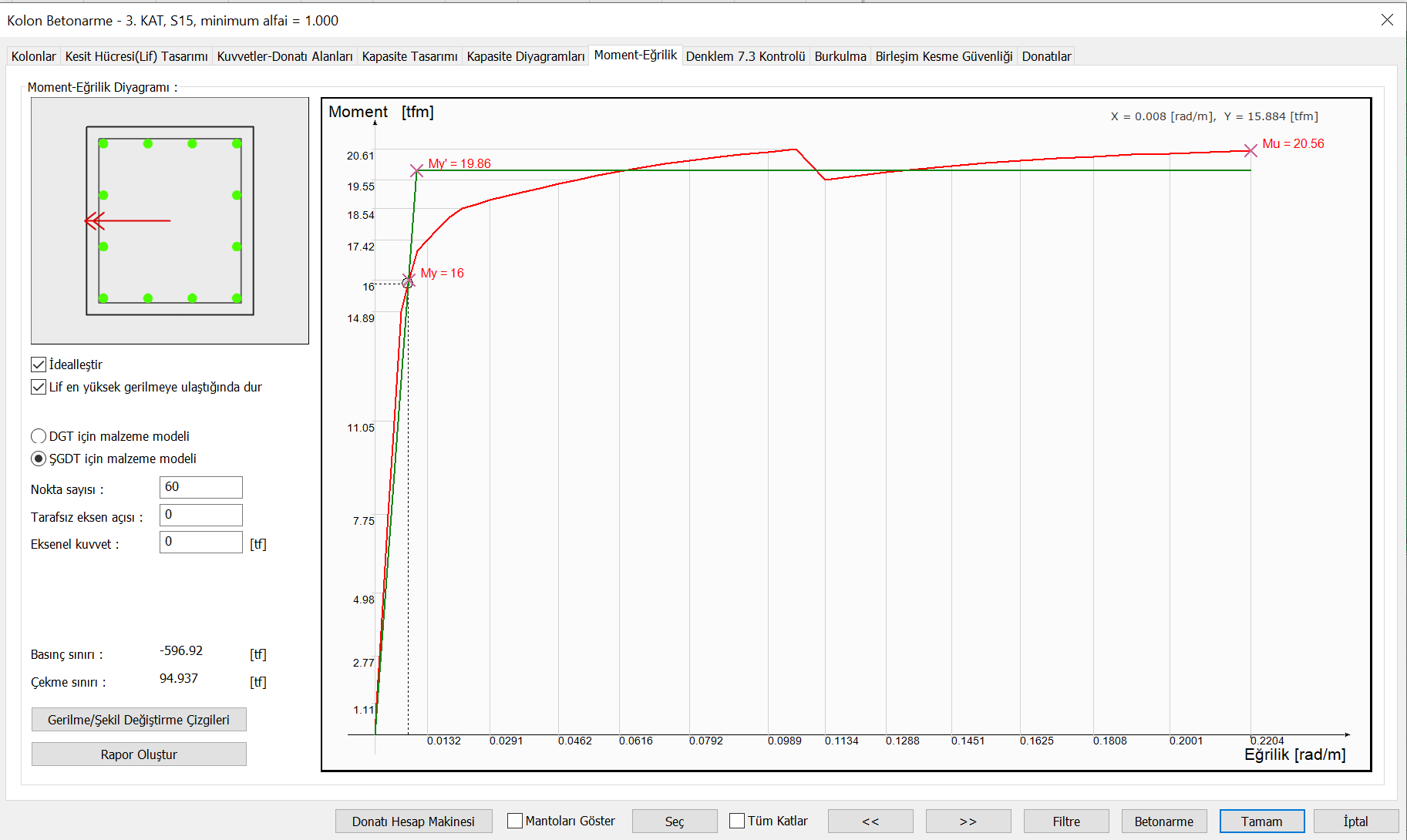
Moment eğrilik analizi sonucu betonarme kesitin akma momenti ve akma eğriliği (My ve ϕy), kesitin göçme momenti ve göçme öncesi eğriliği (Mu ve ϕu), değerleri bulunmaktadır. Aşağıdaki grafikte sünek bir elemanın moment eğrilik grafiği bulunmaktadır.
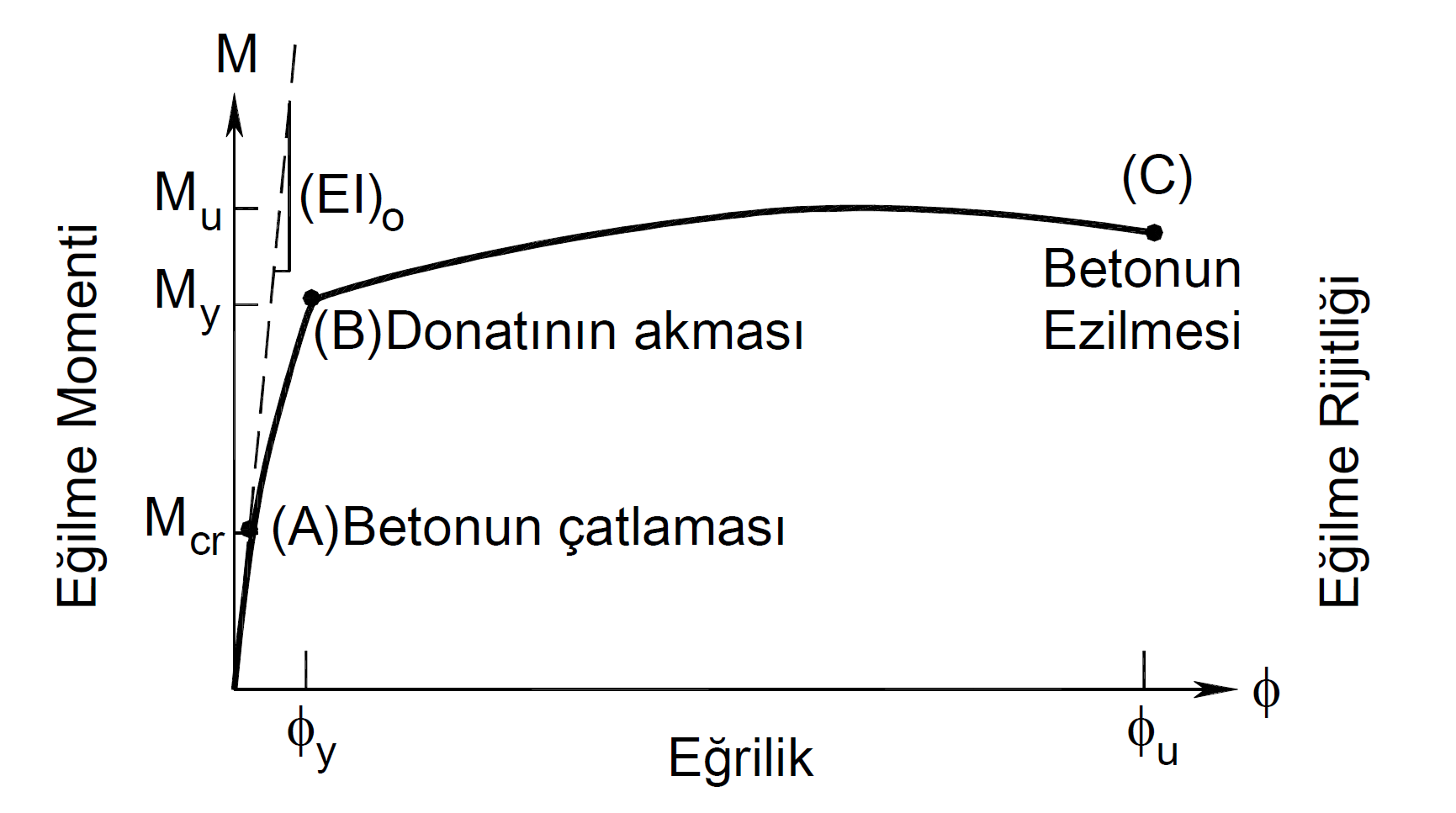
Yukarıdaki resimde gösterilen moment eğrilik grafiğinde My, ϕy noktası çekme eğilme etkisi altındaki betonarme kesitin çekme donatısının aktığı durumdaki moment ve eğriliktir. Bu nedenle My ve ϕy değerlerine akma momenti ve akma eğriliği adı verilmektedir. Kesit bu noktaya geldikten sonra plastik şekildeğiştirmelerin başladığı kabul edilir. Ancak sünek bir eleman için bu noktada beton en büyük birim şekildeğiştirme değerine ulaşmamış olmalıdır. Betonun en yüksek birim şekildeğiştirme değerine veya donatının kopma birim şekildeğiştirme değerine ulaştığı nokta kesit dayınımı yitirdiği nokta olarak kabul edilebilir. Bu nedenle kesitin göçmesi Mu, ϕu noktasında meydana gelmektedir. Bu durumda kesitin sünekliği ϕu/ϕy oranı ile ölçülür. DGT yaklaşımında TS500 'de tanımlanan malzeme modellerine göre moment eğrilik çizildiğinde tasarım momenti Mu, ϕu noktasına karşı gelmektedir.
Moment eğrilik analizinin sonuçlarını etkileyen en önemli değişken malzeme modelleri dir. DGT veya ŞGDT yaklaşımlarında farklı malzeme modelleri kullanıldığından moment-eğrilik bağıntıları birbirlerinden farklı çıkmaktadır. ŞGDT yaklaşımında Mevut binaların değerlendirme ve tasarımı için gerekli malzeme modelleri TBDY Madde 15.2.3 'de yeni yapılacak binalar için kullanılan malzeme modelleri TBDY Madde 5.4.1.5 'de anlatılmıştır. Bu konu ile ilgili detaylı açıklama Genel Modelleme Kuralları ve Beton ve Donatı Çeliği için Gerilme-Şekildeğiştirme Bağıntıları başlıkları altında anlatılmıştır.
Elde ettiğimiz moment eğrilik grafiğinin sonuçlarını plastik mafsal tanımında kullanabilmek için bir idealleştirme yapılmalıdır. Bu nedenle aşağıda siyah renk ile gösterilen moment eğriliği grafiği eşit alanlar prensibi kullanılarak kırmızı çizgi ile idealleştirilmektedir.
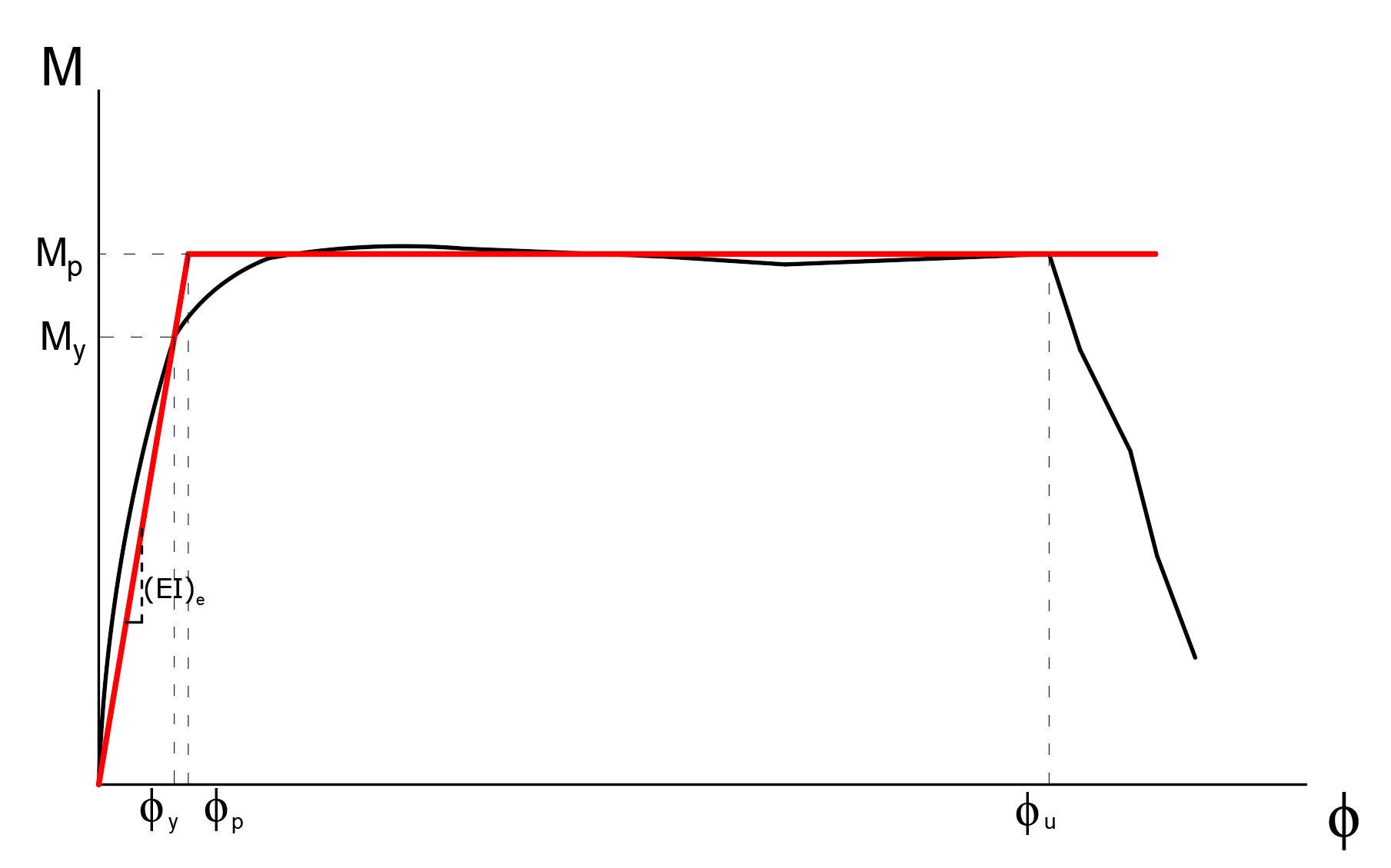
Yukarıdaki grafikte Mp plastik mafsal momenti olarak dikkate alınmaktadır. Herhangi bir doğrusal olmayan analiz yapıldığında plastik mafsal tanımlanan noktadaki eğilme momenti Mp değerine ulaştığında bu noktaya bir plastik mafsal yerleştirilir. Bu nokta üzerindeki moment sabit kalır ancak göçme durumuna gelene dönme şekildeğiştirmesi yapar. Akma momentinden sonra yapılan bu dönme şekildeğiştirmelerine plastik dönme adı verilir ve θ ile gösterilir.
Moment eğrilik bağıntısında kullanılan malzeme modellerinde sargı etkisi dikkate alınmaktadır. ŞGDT yaklaşımında sargı etkisi TBDY Ek 5A ‘da gösterildiği şekli ile dikkate alınmaktadır. Plastik mafsal bölgesindeki kesitin enine donatı koşullarına göre sargı etkisi beton basınç dayanımda bir artış meydana getirmektedir. Aşağıdaki resimde eleman kesiti ve moment eğrilik etkileşimi görülmektedir. ŞGDT yaklaşımında Eleman kesiti’nin iç kısmında (etriye sarılı bölgenin içi) sargılı beton modeli, dış kısmında ise sargısız beton modeli kullanılmaktadır.
Eğrilik ile plastik dönme arasındaki ilişki aşağıda bağıntıda gösterildiği gibidir.
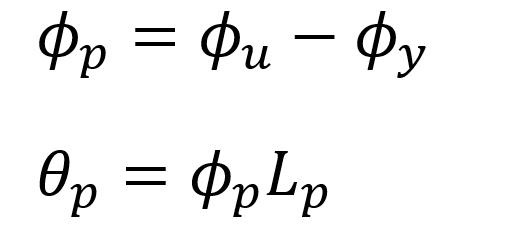
Yukarıdaki bağıntıda ϕp değeri kesitin göçme eğriliğinden akma eğriliğinin çıkartılması ile elde edilen kesitin yaptığı en büyük plastik şekildeğiştirme eğriliğidir. ϕp değeri plastik mafsal boyu, Lp ile çarpıldığında ise plastik dönme istemi diğer bir deyişle plastik mafsalın göçmeden yapabileceği en büyük plastik dönme θp değeri elde edilir. Bu dönme kesitin göçme şekildeğiştirmesidir ve bu noktadan sonra sistem yük taşımaya devam edemez.
Plastik moment, Mp ve plastik dönme istemi, θp moment eğrilik yardımıyla bulunduktan sonra plastik mafsalın iskelet eğrisi aşağıdaki gibi çizilebilir. TBDY Madde 5.3.1.6 'ya göre plastik dönme artışına bağlı olarak plastik momentin artışı terk edilebilir. Bu nedenle eleman plastikleştikten sonra moment sabit kalacaktır. Aşağıdaki grafikte plastik mafsalın iskelet eğrisi gösterilmiştir. Bu grafik yalnızca plastik şekildeğiştirmeleri gösterdiğinden ideal akma momenti veya plastikleşme momenti değerinden küçük momentlerde plastik şekildeğiştirme sıfır olarak gözükecektir. TBDY Madde 5.8.1.2 'de bu iskelet eğrisi üzerindeki plastik şekildeğiştirmelere göre yapı performansı belirlenmektedir.
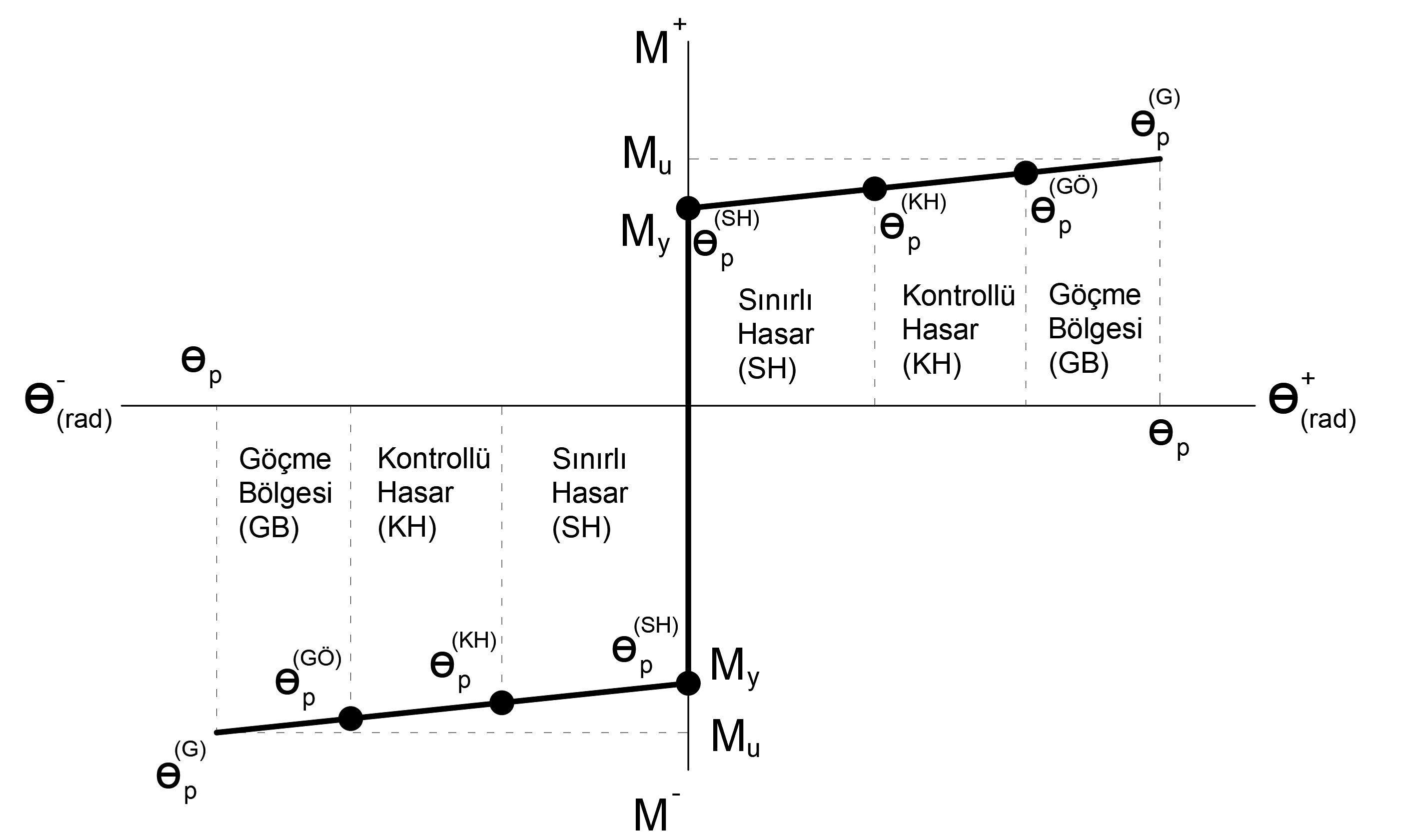
Yukarıda anlatılan konular yalnızca eğilme momenti alan elemanlar için kullanılmaktadır. Ancak eğilme etkisinin yanında normal kuvvetin de etkili olduğu elemanlarda (kolon, perde) normal kuvvet moment-eğrilik bağıntısında değişliklerde sebep olur. Normal kuvvetin seviyesi arttığında elemanın plastik şekildeğiştirme kabiliyeti değişecek bununla beraber göçme durumuna daha farklı bir dönme değerinde ulaşacaktır. Normal kuvvet ile beraber eğilme iki yöndeki eğilme momenti de moment eğrilik bağıntısını değiştirecek bu durum dolaylı olarak kesitin plastik şekildeğiştirme kabiliyetini değiştirecektir.
Normal kuvvetin ve iki eksenli eğilmenin etkili olduğu elemanlarda normal kuvvetin seviyesine göre eksenel kuvvet ve iki eksenli eğilme etkileşimi grafiğine (soğan eğrisi) göre plastik mafsal tanımlanmalıdır. Moment eğrilik analizinde farklı normal kuvvet seviyelerinde kuvvetli ve zayıf eğilme ekseni yönünde (M3 ve M2) akma momenti, My ve akma eğrili ϕy ayrı ayrı bulunarak bir etkileşim eğrisi elde edilmektedir. Analizin her bir adımında plastik mafsal oluşabilecek noktadaki P-M2-M3 değerleri kontrol edilerek kesitin akma eğrisine ulaşıp ulaşmadığı kontrol edilmektedir. P-M2-M3 etkileşim eğrisi Her normal kuvvet seviyesinde akma momenti, My ve dolayısıyla idealleştirilerek elde edilmiş Mp değerlerini temsil etmektedir. Aşağıdaki grafiklerde iki boyutlu ve üç boyutlu eksenlerde normal kuvvet eğilme momenti etkileşimi gösterilmiştir.
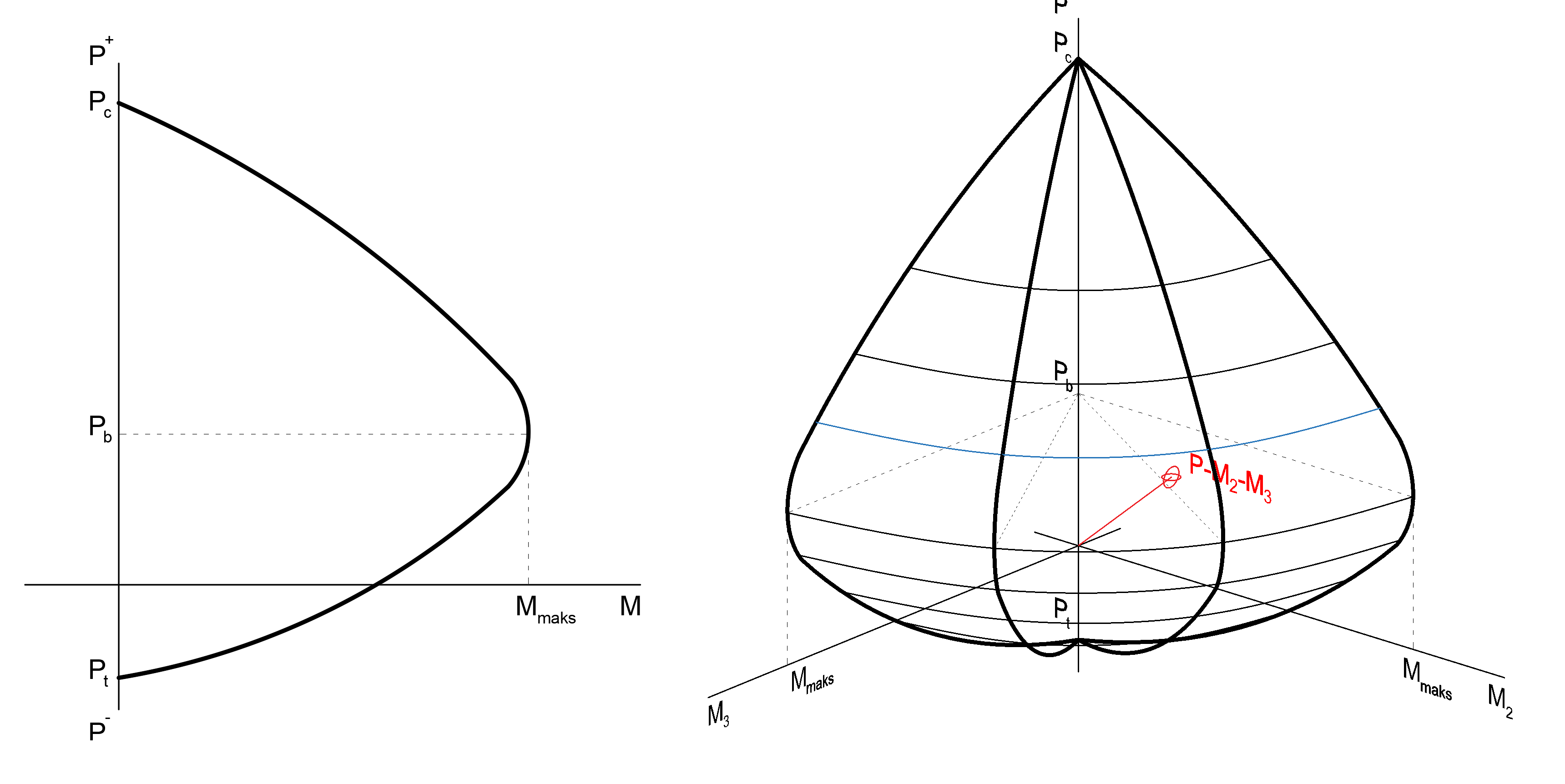
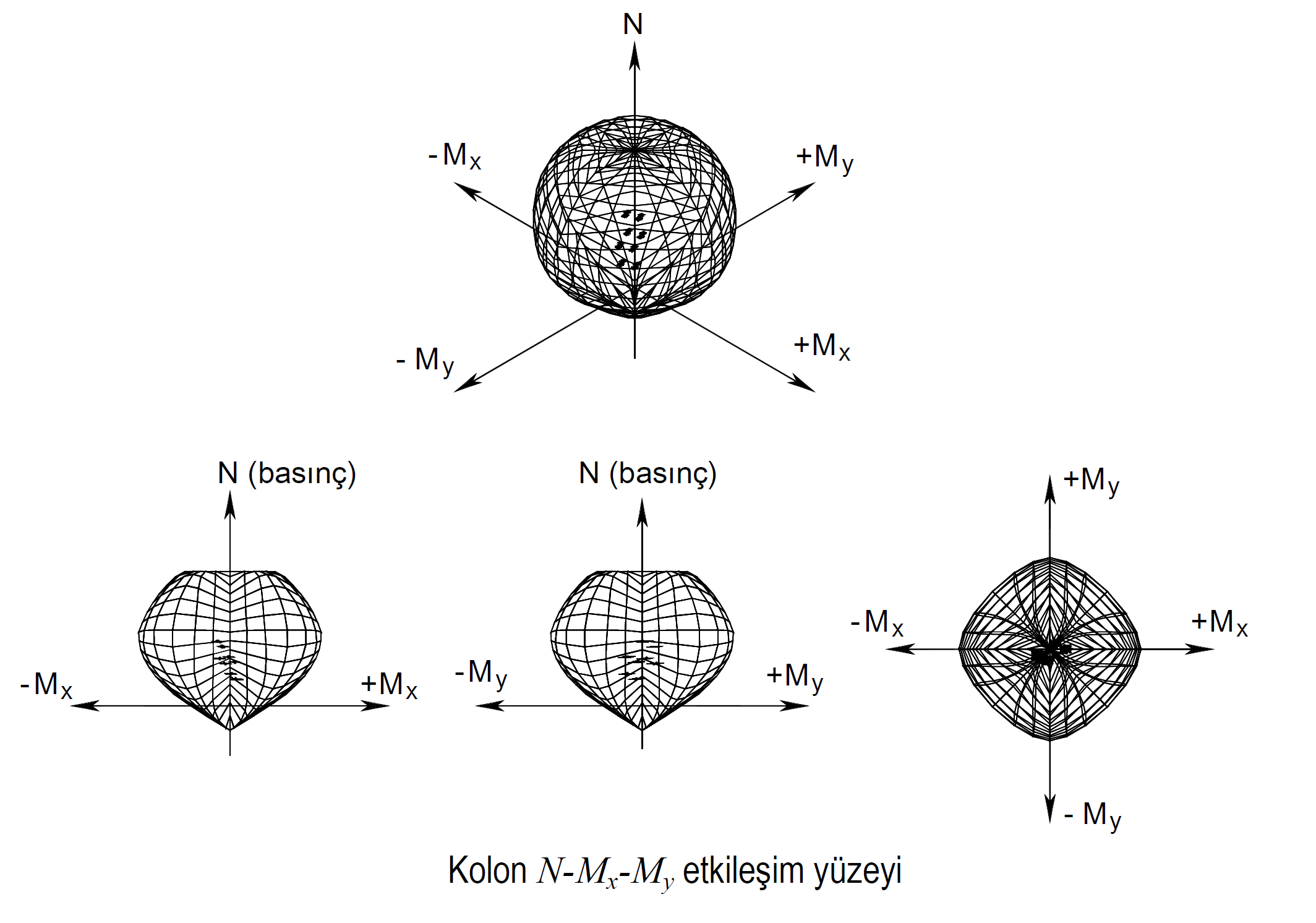
Kirişlerde yalnızca eğilme etkisindeki plastikleşme dikkate alınır. Bu nedenle kirişlerde tanımlanan plastik mafsallara M3 mafsalı adı verilir. Kolon ve perdelerde ise Normal kuvvet ve iki eksenli eğilme etkileşimi olduğunda bu elemanlarda tanımlanan plastik mafsallara PM2M3 mafsalı adı verilir.
Sonraki Konu
