Lokal Ekseni Açılı Çubuk
Bu örnekte global eksen ’e göre açılı tanımlanmış ankastre bir çubuk elemandan oluşan sistemin uç yerdeğiştirmeleri incelenmiş ve ideCAD Statik sonuçları ile karşılaştırılmıştır.
Önemli Not: Bu sistem çözümünde elle çözüm kolaylığı açısından uzama ve kayma deformasyonlarının etkileri ihmal edilmiştir. Uzama şekildeğiştirmelerini ihmal etmek için kesit alanı 1000 ile çarpılmış, kayma şekildeğiştirmelerini ihmal etmek için kayma alanları sıfır “0” olarak tanımlanmıştır.
Yükleme Durumu | Karşılaştırılan Değer | ideCAD Statik | Elle yapılan çözüm | Hata yüzdesi |
|---|---|---|---|---|
| UY (in) | -0.0181 | -0.0181 | %0 |
UZ (in) | -0.0303 | -0.0303 | %0 | |
| UY (in) | -0.0334 | -0.0334 | %0 |
UZ (in) | -0.0561 | -0.0561 | %0 | |
| UY (in) | -0.0836 | -0.0836 | %0 |
UZ (in) | -0.0140 | -0.0140 | %0 |
Geometrik Özellikler ve Sistem Tanımı
Aşağıdaki şekilde 144 in uzunluğunda, global eksene göre 30o döndürülmüş konsol bir elemana ait sistem bilgileri görülmektedir. Global eksenler Y-Z ekseni olarak, lokal eksenler 3-2 ekseni olarak tanımlanmıştır.
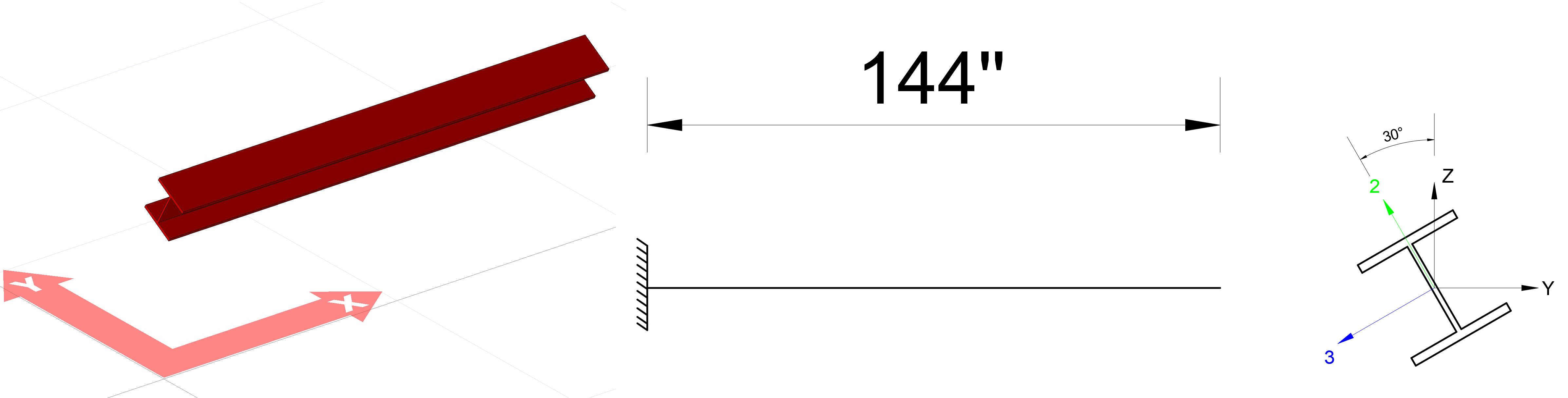
Çubuk eleman olarak W12x106 profil kullanılmıştır. Kesit yüksekliği 12.9 in, kesit genişliği 12.2 in, üst-alt başlık kalınlığı 0.99 ve gövde kalınlığı 0.61 in olarak tanımlanmıştır. Bu durumda;
3 eksenindeki atalet momenti I3 = 933 in4
2 eksenindeki atalet momenti I2 = 301 in4
olarak bulunmuştur. Kullanılan çelik malzemenin Elastisite Modülü E = 29000 k/in2 olarak tanımlanmıştır.
Yükleme durumları
Yukarıda tanımlanan lokal ekseni 30o açıda tanımlanmış konsol elemana 3 adet yükleme durumu tanımlanmıştır. Durum 1, Durum 2 ve Durum 3 olarak adlandırılan bu yükleme durumlarında, elemanın serbest uçlarında global eksene göre Y ve Z eksenlerinde oluşan yerdeğiştirmeler hesaplanacaktır.

Düzgün yayılı yükleme altında konsol elemanın uç yerdeğiştirmesi, tekil yükleme altında konsol elemanının uç yerdeğiştirmesi ve tekil moment etkisi altında konsol elemanının uç yerdeğiştirme denklemleri sırasıyla aşağıda verilmiştir.
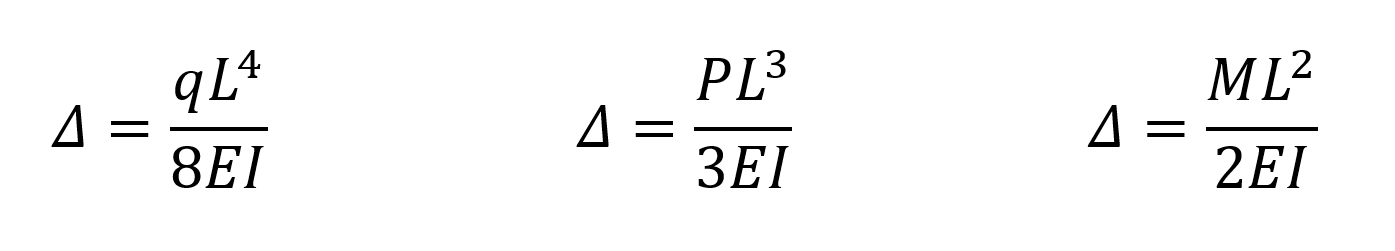
Yukarıdaki bağıntılarda Δ konsol elemanın uç yerdeğiştirme değeri, L konsol eleman uzunluğu, E elastisite modülü, I atalet momenti, q düzgün yayılı yük değeri, P tekil yük değeri ve M tekil moment değeridir. Durum 1, Durum 2 ve Durum 3 için yukarıdaki bağıntılar kullanılabilir. Ancak konsol eleman açılı olarak tanımlandığı ve yük değerleri global eksenlere tanımlandığı için hem Y hem de Z ekseninde ilgili atalet momentleri kullanılarak yukarıdaki bağıntılar hesaplanmalıdır.
Yükleme durumlarının tamamı tanımlanmış dosyaya aşağıdan ulaşabilirsiniz.
Lokal Ekseni Açılı Çubuk Örneği.rar
Durum 1
Yayılı yükleme durumu global Z eksenine göre q=-0.01 k/ft olarak tanımlanmıştır. Bu durumda q yayılı yükleme durumunun elemanın 3 eksenindeki (lokal eksen) bileşeni q33 = q*sin(30) olacaktır. Benzer şekilde q yayılı yükleme durumunun elmanın 2 eksenindeki (lokal eksen) bileşeni q22 = q*cos(30) olacaktır.
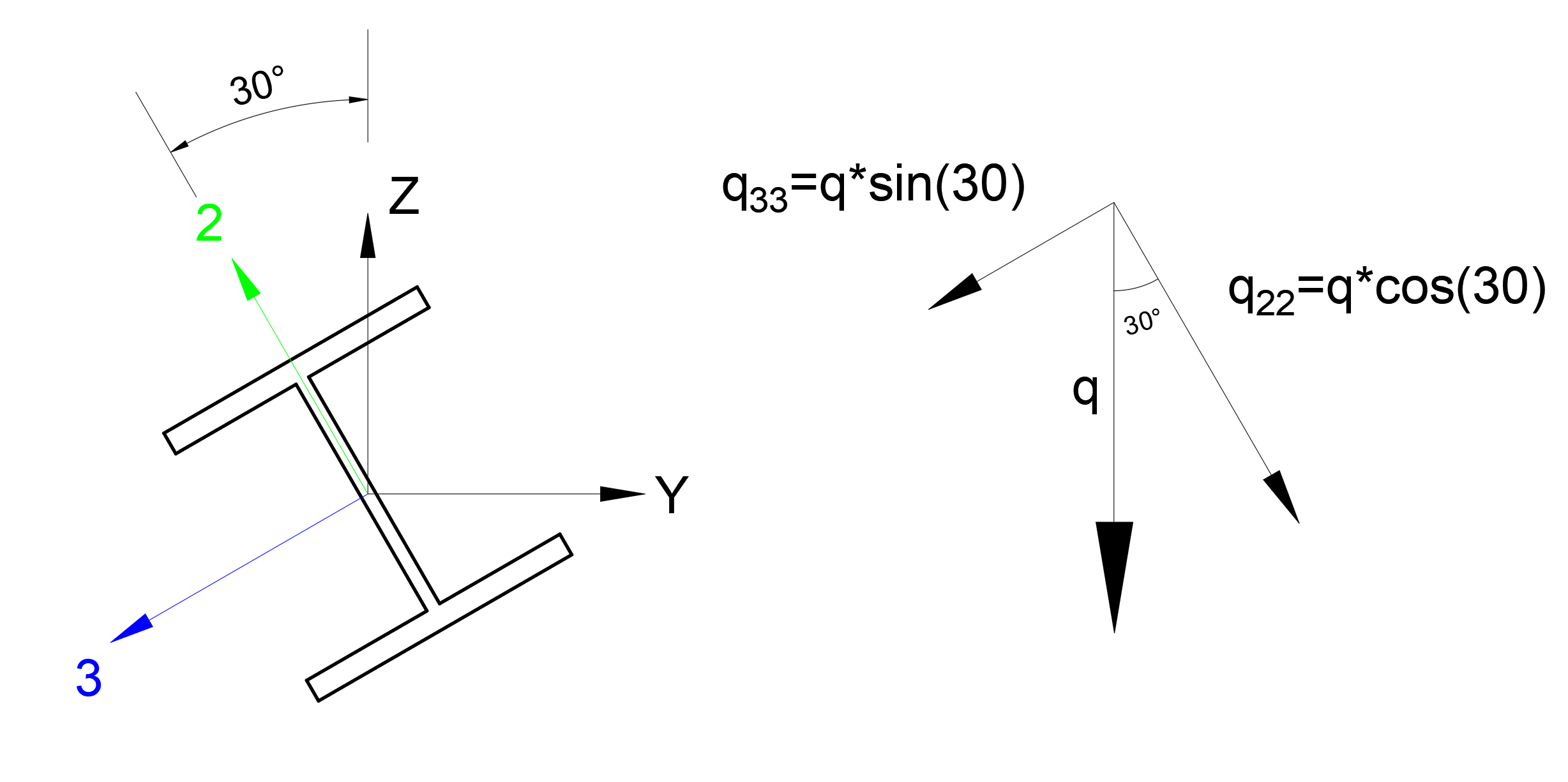
Düzgün yayılı yükleme altında konsol elemanın uç yerdeğiştirmesi Δ değerinin elemanın lokal eksenlerine göre hesabı aşağıdaki gibidir.
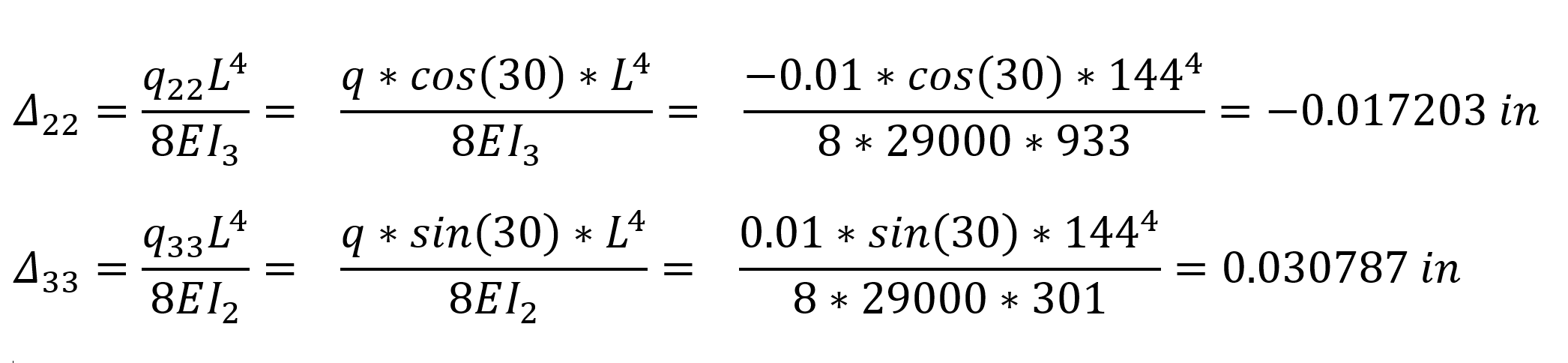
Yukarıdaki bağıntılarda Δ22 elemanın lokal eksenine göre 2 yönündeki yerdeğiştirmesi, Δ33 elemanın lokal eksenine göre 3 yönündeki yerdeğiştirmesidir. Bu değerleri global eksenlere çevirmek için aşağıdaki işlemler uygulanabilir.
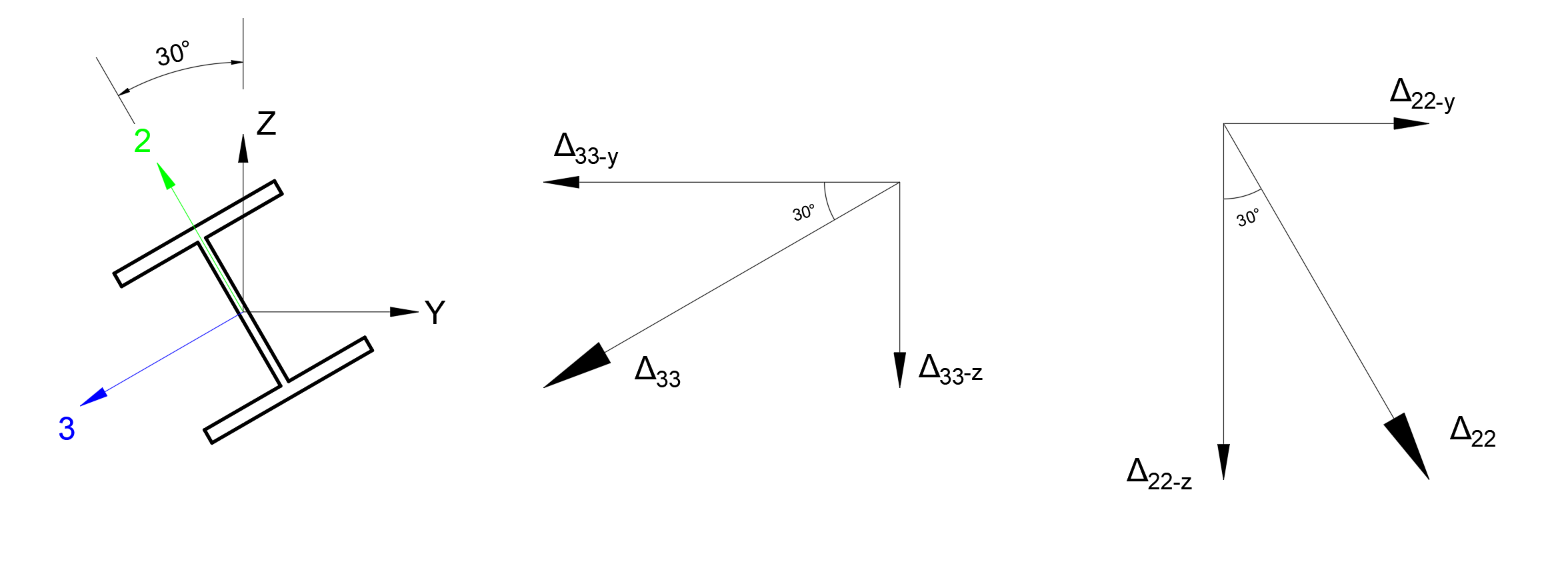
Δ33 yerdeğiştirmesinin z global ekseni üzerindeki izdüşümü Δ33-z = 0.030787 * sin(30) = 0.015393 in
Δ33 yerdeğiştirmesinin y global ekseni üzerindeki izdüşümü Δ33-y = 0.030787 * cos(30) = 0.026662 in
Δ22 yerdeğiştirmesinin z global ekseni üzerindeki izdüşümü Δ22-z = 0.017203 * cos(30) = 0.014898 in
Δ22 yerdeğiştirmesinin y global ekseni üzerindeki izdüşümü Δ22-y = 0.017203 * sin(30) = 0.008602 in
olarak bulunur. Bu yerdeğiştirme değerlerini yüklemelerin yönleri gözönüne alınarak toplandığında;
ΔY = 0.008602 - 0.026662 = -0.0181 in
Δz = -0.015393 - 0.014898 = -0.0303 in
olarak bulunur.
ΔY = -0.0181 in ve Δz = -0.0303 in değerleri ideCAD Statik sonuçları ile birebir aynıdır.

Durum 2
Tekil yükleme durumu global Z eksenine göre P=1 kip olarak tanımlanmıştır. Bu durumda P tekil yükleme durumunun elemanın 3 eksenindeki (lokal eksen) bileşeni P33 = P*sin(30) olacaktır. Benzer şekilde P tekil yükleme durumunun elmanın 2 eksenindeki (lokal eksen) bileşeni P22 = P*cos(30) olacaktır.
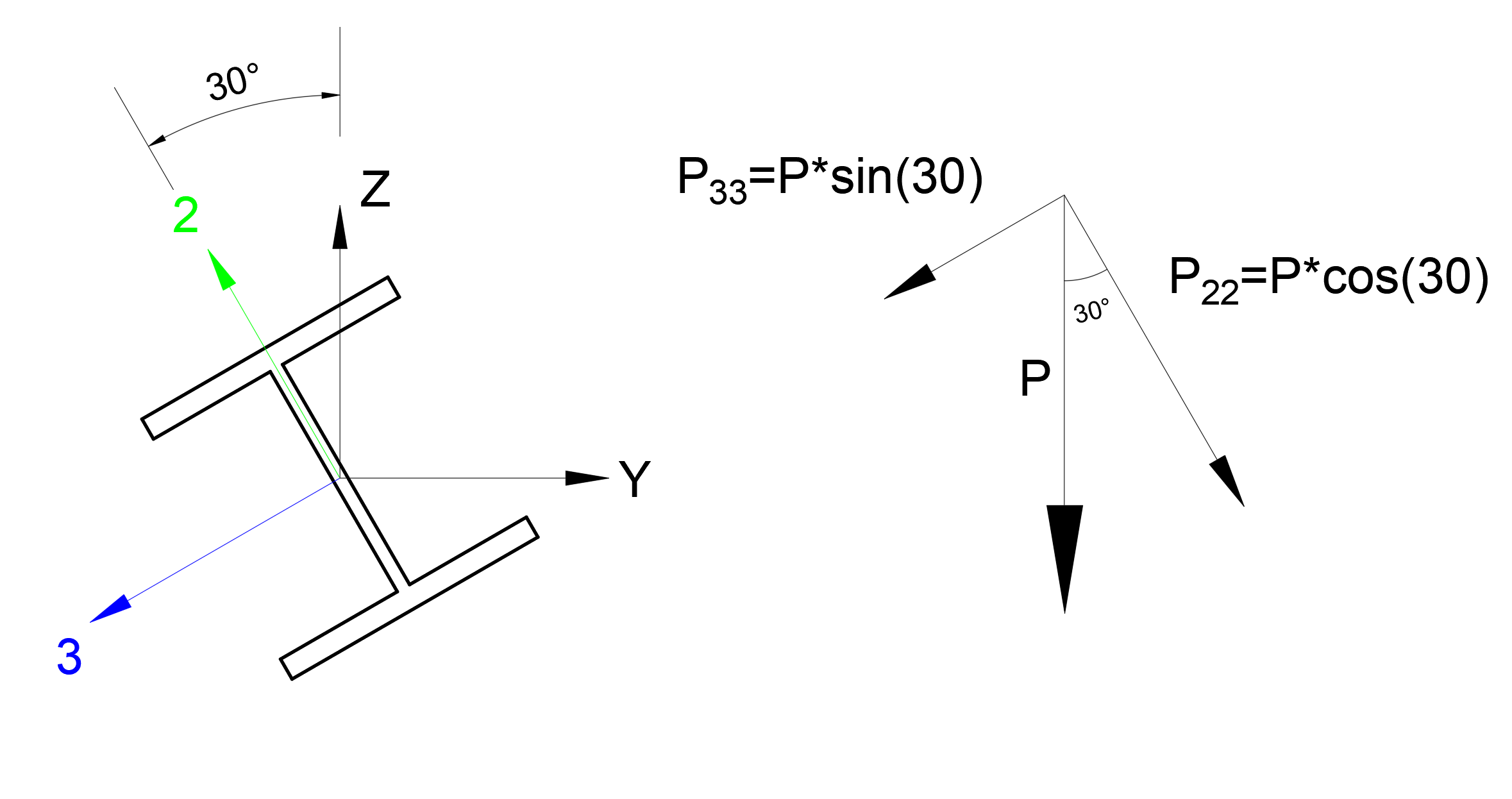
Tekil yükleme etkisi altında konsol elemanın uç yerdeğiştirmesi Δ değerinin elemanın lokal eksenlerine göre hesabı aşağıdaki gibidir.
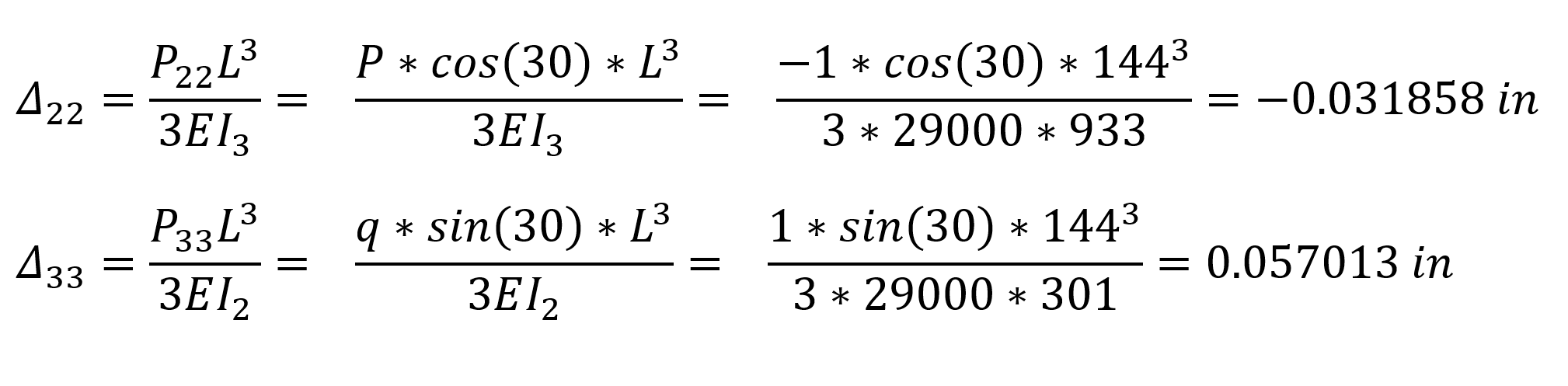
Yukarıdaki bağıntılarda Δ22 elemanın lokal eksenine göre 2 yönündeki yerdeğiştirmesi, Δ33 elemanın lokal eksenine göre 3 yönündeki yerdeğiştirmesidir. Bu değerleri global eksenlere çevirmek için aşağıdaki işlemler uygulanabilir.

Δ33 yerdeğiştirmesinin z global ekseni üzerindeki izdüşümü Δ33-z = 0.057013 * sin(30) = 0.028506 in
Δ33 yerdeğiştirmesinin y global ekseni üzerindeki izdüşümü Δ33-y = 0.057013 * cos(30) = 0.049375 in
Δ22 yerdeğiştirmesinin z global ekseni üzerindeki izdüşümü Δ22-z = 0.031858 * cos(30) = 0.027590 in
Δ22 yerdeğiştirmesinin y global ekseni üzerindeki izdüşümü Δ22-y = 0.031858 * sin(30) = 0.015929 in
olarak bulunur. Bu yerdeğiştirme değerlerini yüklemelerin yönleri gözönüne alınarak toplandığında;
ΔY = 0.015929 - 0.049374 = - 0.0334 in
Δz = -0.027590 - 0.028506 = - 0.0561 in
olarak bulunur.
ΔY = -0.0334 in ve Δz = -0.0561 in değerleri ideCAD Statik sonuçları ile birebir aynıdır.

Durum 3
Tekil moment yükleme durumu global Y ekseni etrafında M=240 k-in olarak tanımlanmıştır. Bu durumda M tekil moment yükleme durumunun elemanın 3 ekseni etrafındaki (lokal eksen) bileşeni M33 = M*cos(30) olacaktır. Benzer şekilde M tekil moment yükleme durumunun elmanın 2 ekseni etrafındaki (lokal eksen) bileşeni M22 = M*cos(30) olacaktır.
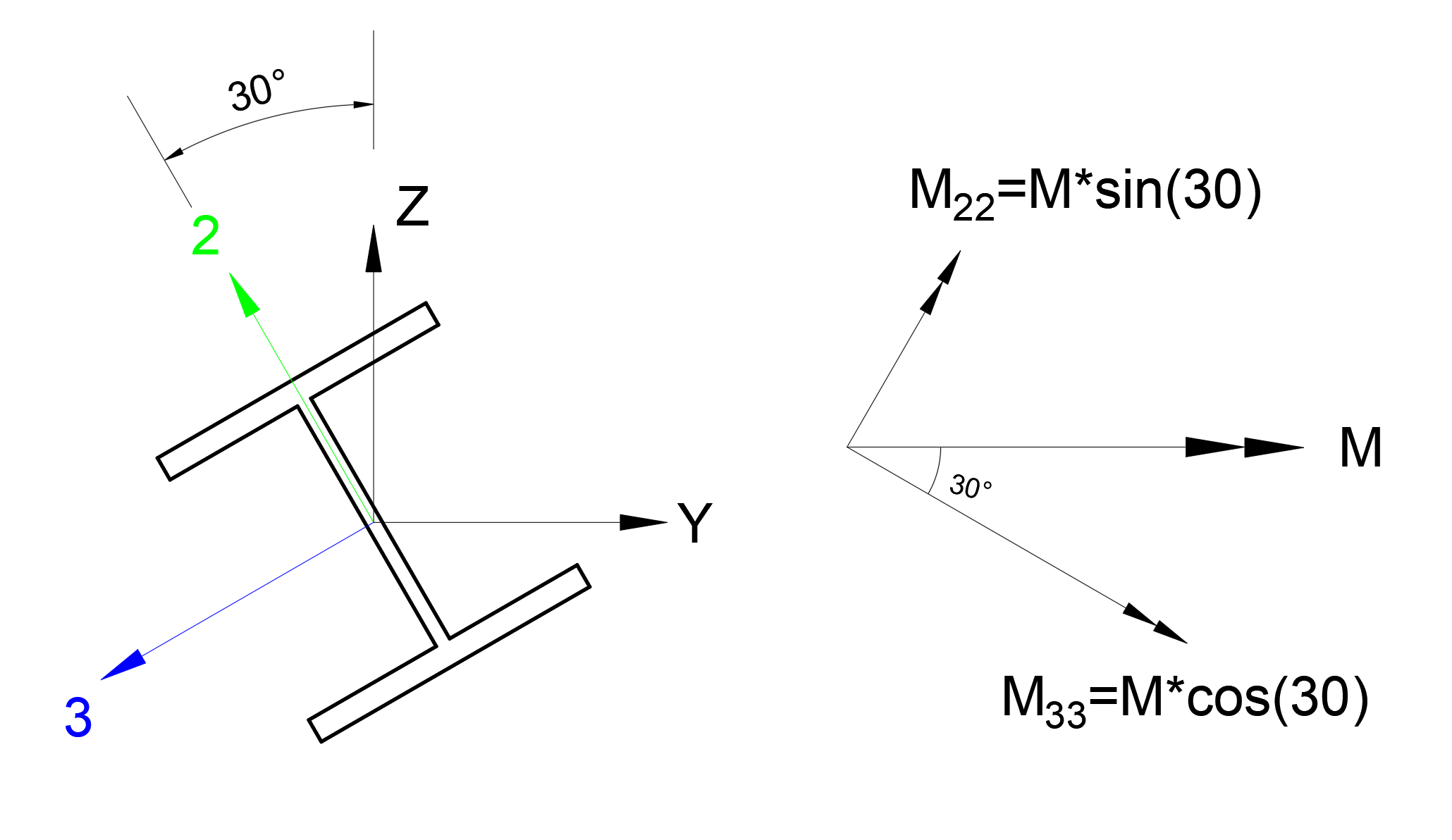
Tekil moment yükleme etkisi altında konsol elemanın uç yerdeğiştirmesi Δ değerinin elemanın lokal eksenlerine göre hesabı aşağıdaki gibidir.
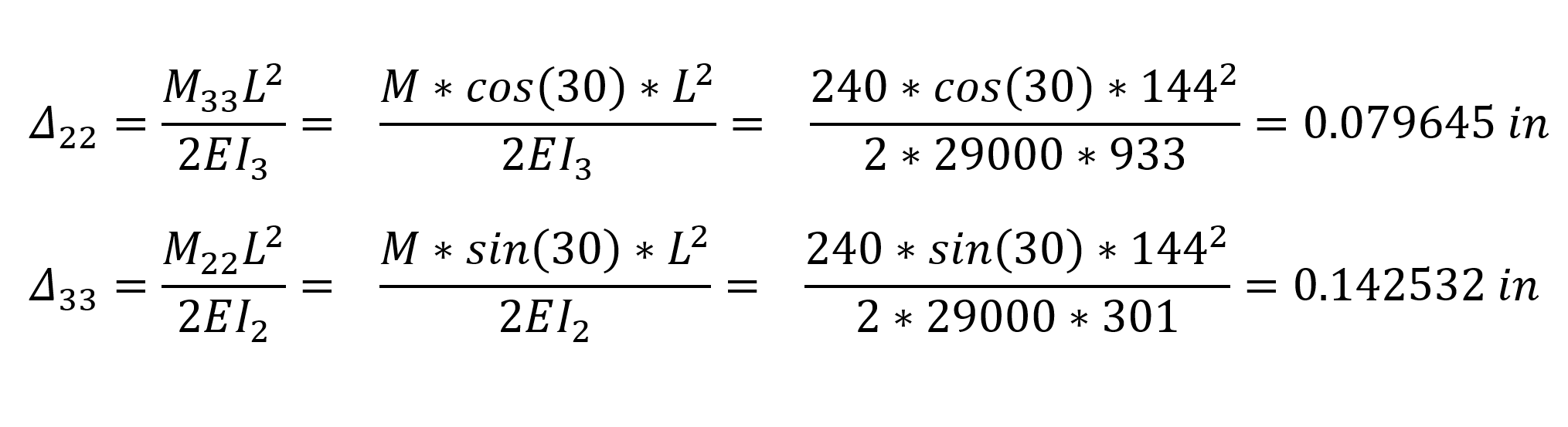
Yukarıdaki bağıntılarda Δ22 elemanın lokal eksenine göre 2 yönündeki yerdeğiştirmesi, Δ33 elemanın lokal eksenine göre 3 yönündeki yerdeğiştirmesidir. Bu değerleri global eksenlere çevirmek için aşağıdaki işlemler uygulanabilir.

Δ33 yerdeğiştirmesinin z global ekseni üzerindeki izdüşümü Δ33-z = 0.142532 * sin(30) = 0.071266 in
Δ33 yerdeğiştirmesinin y global ekseni üzerindeki izdüşümü Δ33-y = 0.142532 * cos(30) = 0.123436 in
Δ22 yerdeğiştirmesinin z global ekseni üzerindeki izdüşümü Δ22-z = 0.079645 * cos(30) = 0.068974 in
Δ22 yerdeğiştirmesinin y global ekseni üzerindeki izdüşümü Δ22-y = 0.079645 * sin(30) = 0.039822 in
olarak bulunur. Bu yerdeğiştirme değerlerini yüklemelerin yönleri gözönüne alınarak toplandığında;
ΔY = 0.039822 - 0.123436 = - 0.0836 in
Δz = -0.068974 - 0.071266 = - 0.0140 in
olarak bulunur.
ΔY = -0.0836 in ve Δz = -0.0140 in değerleri ideCAD Statik sonuçları ile birebir aynıdır.

Sonraki Konu
