Zımbalama Kontrolü Örnek 1
Örnek hesapta boyutları 100x80 olan bir kolon için zımbalama hesabı yapılacaktır. Hesaptaki diğer parametreler aşağıdaki gibi sıralanmaktadır.
Döşeme kalınlığı: 27 cm
Döşeme paspayı: 3 cm
Malzeme: C35/S420
fctd = 1380.42 kN/m2 (Beton tasarım çekme dayanımı)
Döşeme faydalı yüksekliği, d, hesabı;
d = (Döşeme kalınlığı - Döşeme paspayı) = 27 - 3 = 24 cm
Kolon boyutları
c1 = 100 cm c2 = 80 cm
Zımbalama çevresi (up), kolon yüzeyinden d/2 mesafede hesaplanmaktadır ve aşağıdaki resimde gösterilmektedir. Bu durumda zımbalama çevresinin kenarlarını (b1 , b2) bulmak için kolon boyutlarına d eklenerek yapılır.
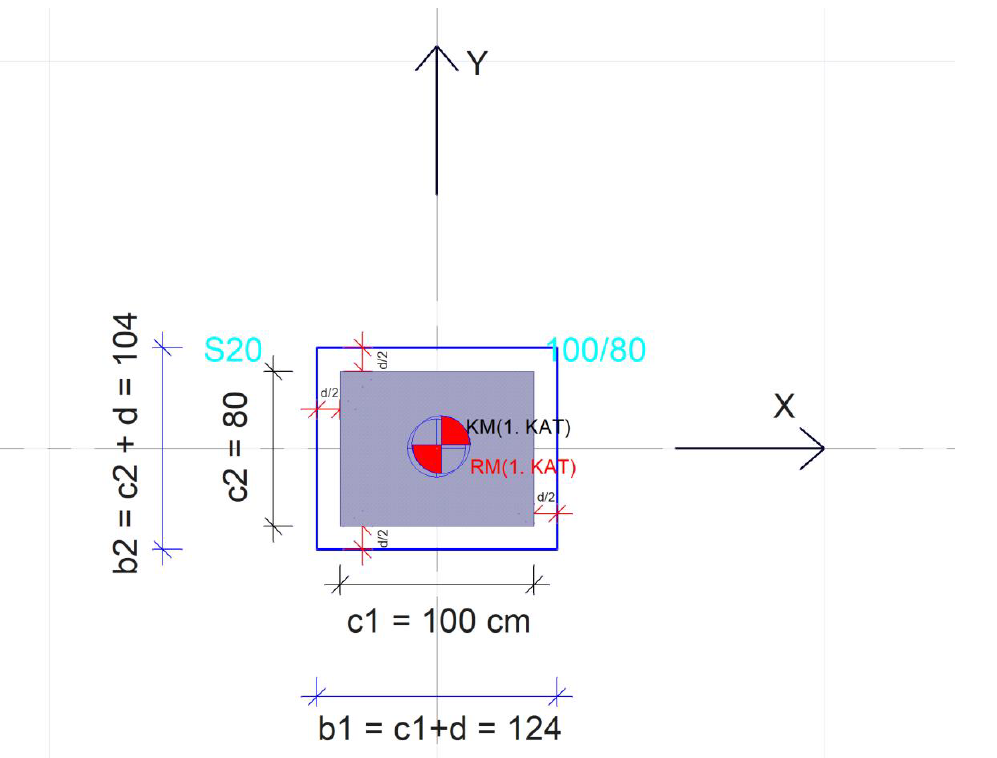
Bu durumda zımbalama çevresi, (up) , ve zımbalama çevresinin döşeme faydalı yüksekliği, d, ile çarpılması ile elde edilen zımbalama alanı (Az) aşağıda gösterildiği gibi hesaplanır.
Aşağıda çizilen kayma gerilmeleri, döşeme düzlemine dik zımbalama gerilmeleridir.
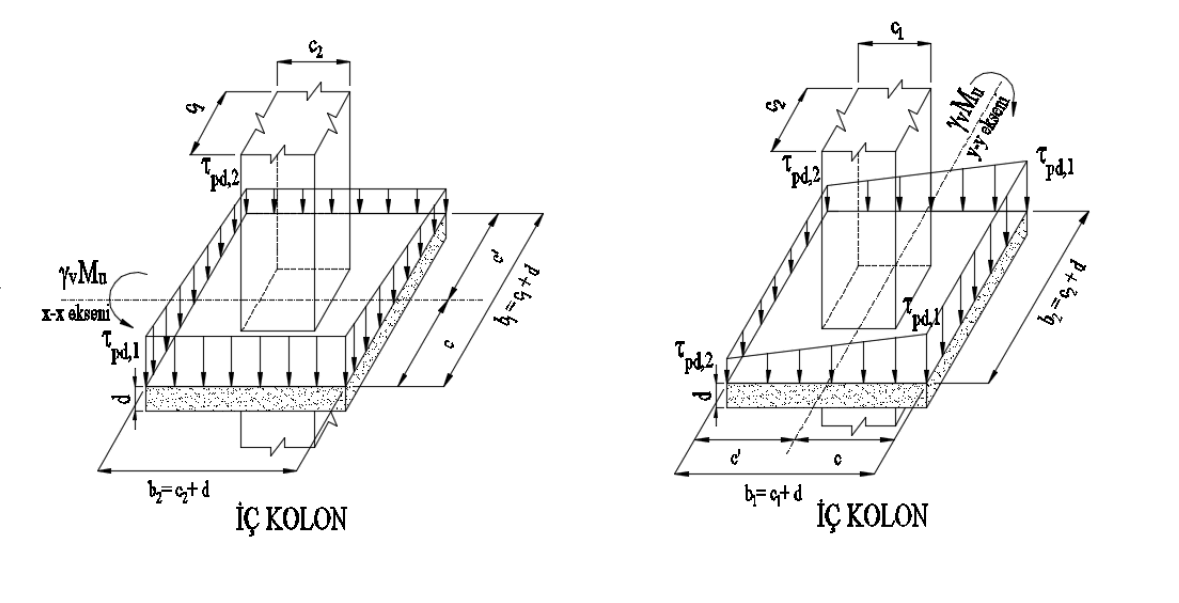
J değerleri, zımbalama alanını (Az) oluşturan yüzeylerin polar atalet ve ikinci atalet momentlerinin toplamıdır. Bu değer TBDY Denklem 7.28 'e göre γf katsayısı gözönüne alınan yükleme doğrultusuna göre hesaplanır.
Kuvvetli Eksen ( Major Yön ) İçin J ve γf Katsayısı Hesabı
γf(maj) ve γv(maj) katsayıları aşağıdaki gibi hesaplanır.
J(maj) değerini bulmak için aşağıdaki işlemler yapılır.
c(maj) , kesitin kuvvetli eksenindeki J değeri ( J(maj) ) bulunurken ele alınan ve moment vektörüne dik ağırlık merkezi mesafesidir. Zımbalama çevresi dikdörtgen olduğundan;
Polar atalet ve ikinci atalet momentleri sırasıyla aşağıdaki gibi hesaplanır.
Bu durumda kesitin kuvvetli (major) eksenine göre olan polar atalet ve ikinci atalet momentlerinin toplamı J(maj) aşağıdaki gibi bulunmaktadır.
Zayıf Eksen ( Minor Yön ) İçin J ve γf Katsayısı Hesabı
γf(min) ve γv(min) katsayısı hesabı için aşağıdaki adımlar izlenir.
J(min) değeri aşağıdaki gibi bulunur.
c(min) değeri, kesitin zayıf eksenindeki J değeri ( J(min) ) bulunurken ele alınan ve moment vektörüne dik ağırlık merkezi mesafesidir. Zımbalama çevresi dikdörtgen olduğundan;
Bu durumda polar atalet ve ikini atalet momentleri sırasıyla aşağıdaki gibi bulunur.
Bu durumda kesitin zayıf (minor) eksenine göre olan polar atalet ve ikinci atalet momentlerinin toplamı J(min) aşağıdaki gibi bulunmaktadır.
Zımbalama Gerilmelerinin Bulunması
Zımbalama gerilmeleri için ele alınacak kuvvetler ve elde geometriden elde edilen değerler aşağıda verilmiştir.
Vd = 683.13 kN
DMd(maj) = 143.53 kNm
DMd(min) = 546.65 kNm
Az = 1.0944 m2
γf(maj) = 0.579
γv(maj) = 0.421
γf(min) = 0.621
γv(min) = 0.379
J(maj) = 0.27101448 m4
J(min) = 0.2083328 m4
c(maj) = 0.62 m
c(min) = 0.52 m
c'(maj) = 0.62 m
c'(min) = 0.52 m
Yukarıda bulunan tüm değerler, zımbalama tasarımına esas iç kuvvetler ile birlikte gerilme formüllerinde yerine konularak zımbalama gerilmeleri bulunur.
τpd,1 , τpd,2 değerlerinden mutlak değerce en büyük olan τpd,1 = 1279.56 kN/m2 değeridir. Elde edilen bu değer, beton tasarım çekme dayanımı olan fctd değeri ile karşılaştırılır.
τpd,1 = 1279.56 kN/m2 < fctd = 1380.42 kN/m2
Döşeme zımbalama dayanımı yeterlidir. Rapor sonuçları ile de bu değerler karşılaştırılabilir.
Sonraki Konu
