Toplam Eğrilik Talebi (15.5.4.2)
Toplam eğrilik talebi, doğrusal performans analizi yapılırken hesaplanan yerdeğiştirmiş eksen dönmesi, moment eğrilik bağıntısı kullanılarak hesaplanan akma momenti ve akma eğriliği değerleri kullanılarak elde edilir.
Eleman uç kesitinin toplam eğrilik talebi ϕt , otomatik hesaplanır.
SİMGELER
E = Beton elastisite modülü
h = Kesit yüksekliği
I = Atalet momenti
Lp = Plastik mafsal boyu
lc = Eleman net açıklığı
My = Etkin akma momenti
Myi = i ucundaki etkin akma momenti
Myj = j ucundaki etkin akma momenti
Δ = Eleman düğüm noktaları arası öteleme
ϕy = Akma eğriliği
ϕt = Toplam eğrilik
θp = Plastik dönme talebi
θy = Akma dönmesi
θyi = i ucundaki akma dönmesi
θyj = j ucundaki akma dönmesi
θk = Yerdeğiştirmiş eksen dönmesi
θki = i ucundaki yerdeğiştirmiş eksen dönmesi
Mevcut binaların Şekildeğiştirmeye Göre Değerlendirme ve Tasarım (ŞGDT) yaklaşımı ile deprem performansının belirlenmesinde doğrusal hesap yöntemi kullanılıyor ise eleman uç kesitinin toplam eğrilik talebi ϕt , Denk.(15.2) ile hesaplanmaktadır.
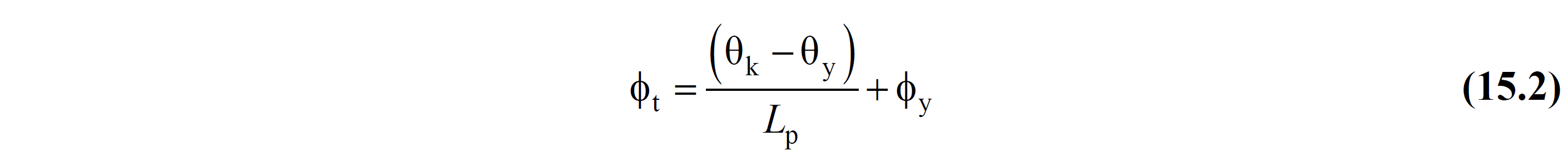
Bu denklemde θk , yerdeğiştirmiş eksen dönmesini ifade eder ve Denk.(15A.1) ile hesaplanmaktadır.
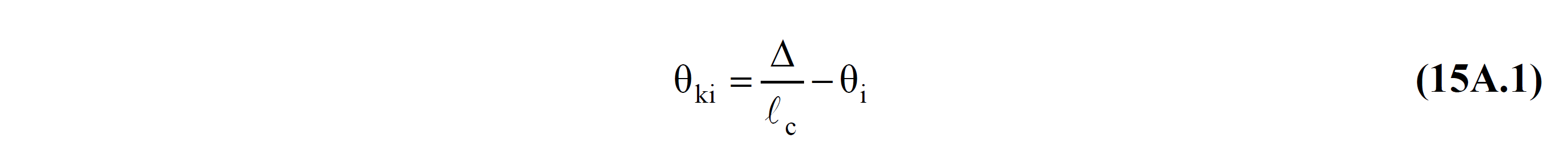
θy , akma dönmesini ifade eder. Deprem performansının belirlenmesinde doğrusal hesap yöntemi kullanılıyor ise bu akma dönmesi TBDY 15A.3 'de belirtilen Çerçeve Elemanlarda Akma Dönmesi ve TBDY 15A.4 'de belirtilen Perde Elemanlarında Akma Dönmesi bağıntıları ile hesaplanmaktadır.
TBDY Bölüm 15A.3 'de belirtilen her iki ucunda akma durumuna geçen bir eğilme çerçeve elemanının i ve j uçlarındaki akma dönmeleri ve uç momentleri arasındaki ilişki Denk.(15A.3) 'de verilmiştir. EI çatlamamış kesite ait eğilme rijitliğidir. Myi ve Myj sırasıyla i ve j uçlarındaki etkin akma momentleri 'dir. Myi ve Myj kesit malzeme modeli ve donatı yerleşimine göre hesaplanan moment-eğrilik bağıntısı ile hesaplanır.
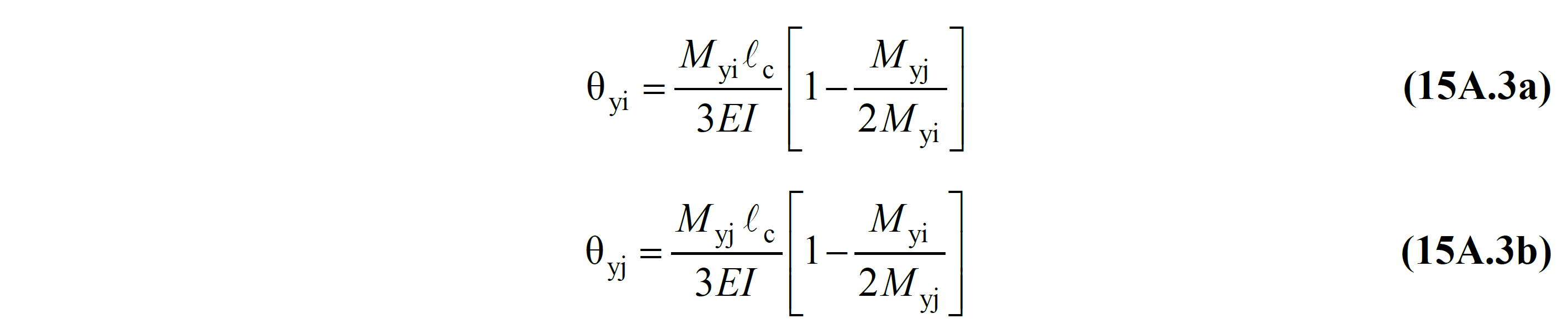
TBDY Bölüm 15A.4 'de ve perde olarak tanımlanan bir eğilme elemanının binanın herhangi bir katındaki alt ucunda akma dönmesi ve akma momenti arasındaki ilişki Denk.(15A.4) 'de verilmiştir. EI çatlamamış kesite ait eğilme rijitliğidir. My etkin akma momenti 'dir. Perde kesitinin malzeme modeli ve donatı yerleşimine göre hesaplanan moment-eğrilik bağıntısı ile hesaplanır.
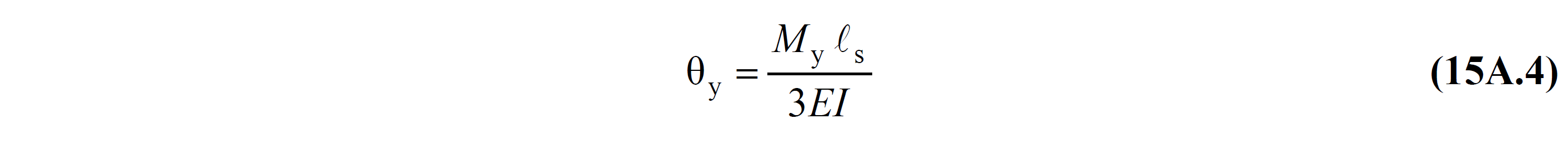
Denk.(15.2) 'de ϕy ile ifade edilen terim eleman uç kesitindeki akma eğriliğidir. ϕy değeri kesit malzeme modeli ve donatı yerleşimine göre hesaplanan moment-eğrilik bağıntısı ile bulunur. Aşağıdaki moment-eğrilik grafiğinde ( B ) noktası donatının akması durumundaki moment My ve donatının akması durumundaki eğrilik ϕy 'dir. Çizilen bu moment-eğrilik bağıntısı bilgi düzeyi katsayısı ile mevcut malzeme dayanımları gözönüne alınarak oluşturulan malzeme modelleri ile oluşturulmaktadır.
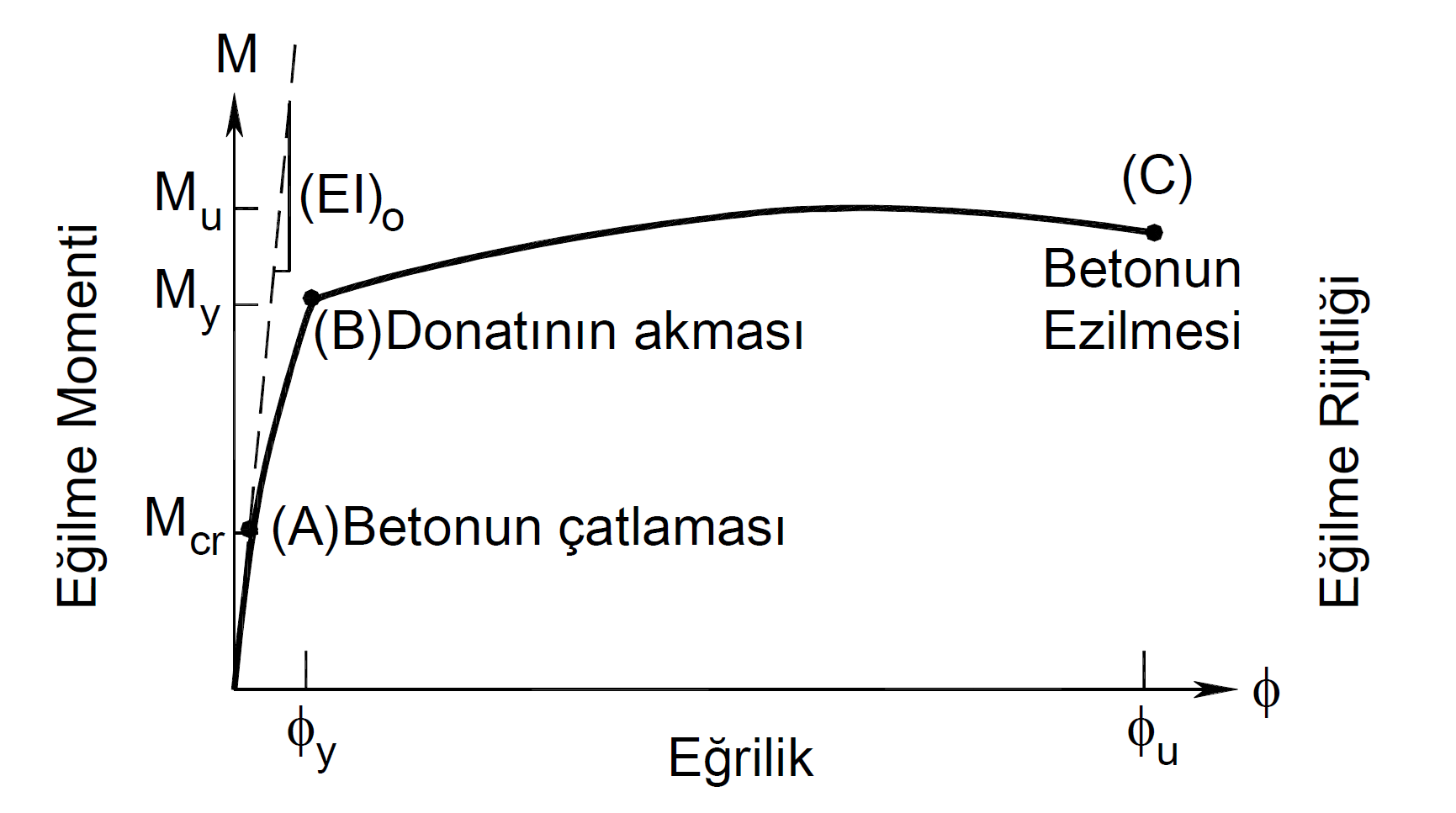
Denk.(15.2) 'de Lp plastik mafsal boyudur ve etkili doğrultudaki kesit yüksekliğinin yarısı olarak hesaplanmaktadır.
Aşağıdaki rapor örneğinde kirişler için toplam eğrilik talebi ϕt , akma dönmesi θy , akma momenti My , plastik dönme talebi θp , akma eğriliği ϕy , toplam eğrilik talebi ϕt gösterilmiştir.
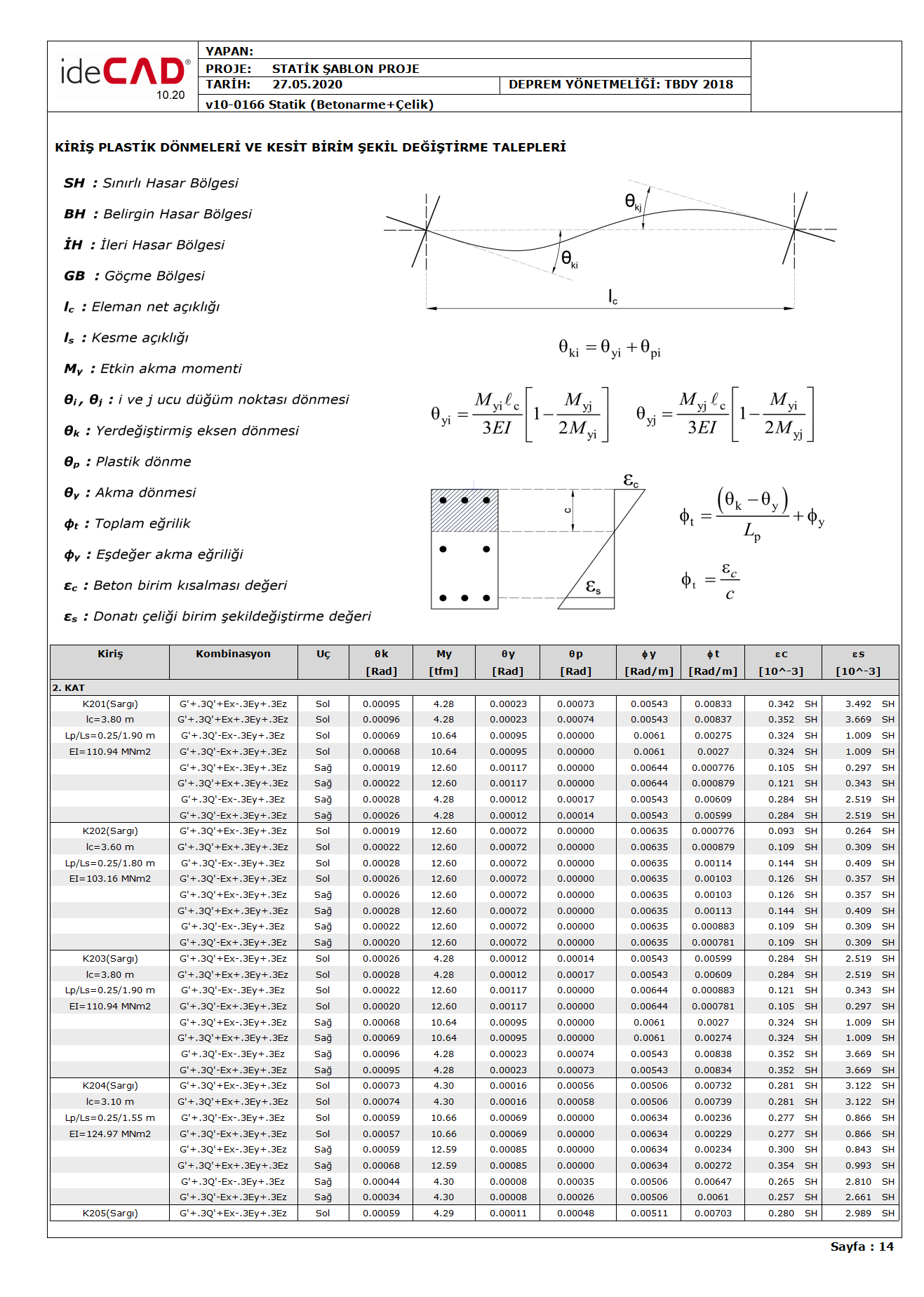
Aşağıdaki rapor örneğinde kolonlar için toplam eğrilik talebi ϕt , akma dönmesi θy , akma momenti My , plastik dönme talebi θp , akma eğriliği ϕy , toplam eğrilik talebi ϕt gösterilmiştir.

Sonraki Konu
